Interior Himpunan

Dalam ruang topologi \( X \), interior dari himpunan \( A \) adalah gabungan semua himpunan terbuka yang seluruhnya berada di dalam \( A \). Notasi yang biasa digunakan adalah \( \text{Int}(A) \) atau \( A^\circ \).

Konsep ini membantu kita memahami bagian mana dari suatu himpunan yang benar-benar berada “di dalam”, tanpa menyentuh batasnya. Interior memberikan himpunan terbuka terbesar yang seluruh elemennya masih berada dalam \( A \).

Tidak ada himpunan terbuka lain di dalam \( A \) yang lebih besar daripada interiornya, sehingga interior dapat dipandang sebagai inti terbuka dari \( A \).

Catatan: Karena interior didefinisikan sebagai gabungan himpunan terbuka, hasil akhirnya selalu berupa himpunan terbuka.

Secara formal, interior \( A \) terdiri atas semua titik yang memiliki lingkungan terbuka yang sepenuhnya berada di dalam \( A \):

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ terbuka dalam } X \} $$

Artinya, jika suatu titik termasuk dalam interior, maka kita dapat menemukan himpunan terbuka yang memuat titik tersebut dan tidak keluar dari batas \( A \).

Perlu diingat bahwa interior sangat dipengaruhi oleh topologi yang digunakan. Himpunan yang sama dapat memiliki interior yang berbeda jika struktur topologinya diubah.

Contoh Praktis

Ambil himpunan \( A = [0, 1] \) dalam \( \mathbb{R} \) dengan topologi standar. Interval ini mencakup semua titik dari 0 hingga 1.

Dalam topologi standar, interiornya adalah interval terbuka \( (0,1) \):

$$ \text{Int}(A) = (0,1) $$

Titik 0 dan 1 tidak termasuk karena tidak ada interval terbuka yang sepenuhnya berada di dalam \( A \) dan memuat titik-titik tersebut.

Contoh 2

Pertimbangkan sekarang \( A = [0,1) \). Walaupun batas kanannya terbuka, interiornya tetap sama, yaitu \( (0,1) \).

\[ \text{Int}(A) = (0,1) \]

Hasil ini muncul karena interior selalu mencari himpunan terbuka terbesar yang benar-benar berada di dalam \( A \), bukan berdasarkan sifat titik batas kiri atau kanannya.

Catatan: Dalam topologi standar, interval terbuka seperti \( (0,1) \) menjadi acuan dasar untuk seluruh himpunan terbuka. Tidak ada interval terbuka yang memuat titik 0 dan tetap sepenuhnya berada di dalam \( A = [0,1) \).

Contoh 3

Jika kita beralih ke topologi diskret, situasinya berubah drastis. Dalam topologi ini, setiap himpunan bagian dianggap terbuka.

Untuk \( A = [0,1) \), hal ini berarti seluruh himpunan tersebut terbuka, sehingga interiornya sama dengan dirinya sendiri:

$$ \text{Int}(A) = A = [0,1) $$

Fenomena ini khas topologi diskret, di mana semua himpunan bersifat terbuka tanpa syarat.

Catatan: Contoh ini menyoroti bagaimana perubahan topologi dapat mengubah total struktur interior sebuah himpunan.

Contoh 4

Sekarang perhatikan ruang topologi kecil \( X = \{a, b, c\} \) dengan topologi diskret. Semua himpunan bagian dalam ruang ini terbuka, mulai dari himpunan kosong hingga himpunan penuh.

• Himpunan \( \emptyset \) dan \( \{a, b, c\} \) terbuka.
• Himpunan satu titik seperti \( \{a\} \), \( \{b\} \), dan \( \{c\} \) terbuka.
• Himpunan dua titik seperti \( \{a, b\} \), \( \{a, c\} \), dan \( \{b, c\} \) juga terbuka.

Jika kita ambil \( A = \{b, c\} \), maka interiornya adalah gabungan semua himpunan terbuka yang berada di dalamnya:

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b,c\} = \{b,c\} \]

/id/math/sifat-komplemen-antara-interior-dan-penutupan-suatu-himpunanGabungannya tepat sama dengan \( A \), sehingga interiornya adalah \( A \) sendiri.

Catatan: Dalam topologi diskret, setiap himpunan merupakan interior dirinya sendiri. Tidak ada himpunan yang “kehilangan titik” ketika kita menghitung interiornya.

Teorema Interior Himpunan

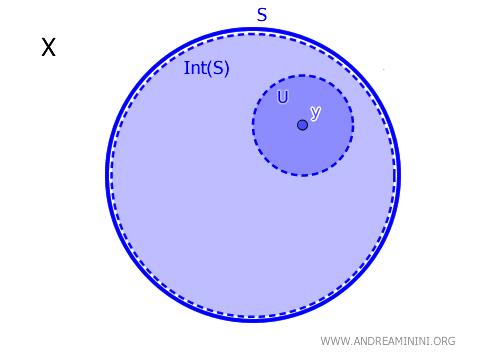
Dalam ruang topologi $X$, titik $y \in X$ berada di dalam interior suatu himpunan $S$, yang dinotasikan $\text{Int}(S)$, jika dan hanya jika terdapat himpunan terbuka $U$ sehingga $y \in U$ dan $U$ seluruhnya berada di dalam $S$. Secara formal, $$ y \in \text{Int}(S) \iff \exists \ U \text{ terbuka dengan } y \in U \subseteq S $$

Teorema ini memberikan cara yang sangat efektif untuk mengenali apakah suatu titik benar-benar berada “di dalam” suatu himpunan. Suatu titik disebut interior apabila kita dapat menempatkannya dalam sebuah lingkungan terbuka yang tidak keluar dari batas himpunan tersebut.

Dengan karakterisasi ini, memeriksa keanggotaan interior menjadi proses yang jelas dan terstruktur, terutama dalam analisis topologis yang lebih luas.

Bukti

• Syarat perlu: Jika \(y\) adalah titik interior \(S\), maka berdasarkan definisi terdapat himpunan terbuka \(U\) yang memuat \(y\) dan seluruhnya berada di dalam \(S\). Hal ini memastikan bahwa setiap titik interior selalu memiliki lingkungan terbuka yang sesuai.
• Syarat cukup: Jika terdapat himpunan terbuka \(U\) dengan \(y \in U \subseteq S\), maka titik \(y\) otomatis merupakan titik interior. Alasannya sederhana: interior adalah gabungan semua himpunan terbuka yang berada dalam \(S\), sehingga setiap titik dalam himpunan terbuka tersebut termasuk interior.

Catatan: Teorema ini menjadi alat utama dalam topologi karena menghubungkan konsep “terbuka” dengan struktur internal himpunan. Pendekatan ini banyak digunakan dalam kajian kontinuitas, pemetaan topologis, dan struktur ruang yang lebih kompleks.

Contoh

Tinjau himpunan \( A = [1,3] \) dalam ruang real \( \mathbb{R} \) dengan topologi standar.

$$ A = [1,3] $$

Himpunan ini mencakup seluruh titik real antara 1 dan 3. Untuk menentukan interiornya, kita cukup mencari himpunan terbuka terbesar yang sepenuhnya berada dalam \( A \).

1. Menentukan himpunan kandidat
   Pilihan yang alami adalah interval terbuka \( U = (1,3) \). Interval ini terbuka dalam topologi standar dan tidak mencakup titik batas.
2. Memverifikasi inklusi
   Semua titik dalam \( (1,3) \) juga merupakan titik dalam \( [1,3] \). Titik 1 dan 3 tidak ikut serta karena tidak termasuk interval terbuka.

Karena \( U \subseteq A \) dan merupakan himpunan terbuka terbesar yang memenuhi syarat, diperoleh bahwa:

$$ \operatorname{Int}(A) = (1,3) $$

Catatan: Titik batas 1 dan 3 tidak dapat menjadi titik interior, sebab tidak ada interval terbuka yang memuat salah satu dari titik tersebut tanpa keluar dari \( A \).

Sifat-Sifat Interior

Sifat-sifat berikut menggambarkan bagaimana interior berperilaku terhadap operasi dasar seperti gabungan, irisan, serta hubungan dengan komplemen dan penutup. Sifat-sifat ini penting untuk memahami dinamika struktur ruang topologis secara lebih mendalam.

• Gabungan Interior
  Gabungan interior dua himpunan selalu merupakan bagian dari interior gabungan keduanya: $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$ Meskipun demikian, biasanya inklusi ini tidak bersifat setara.
• Irisan Interior
  Interior irisan dua himpunan identik dengan irisan interior keduanya: $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
• Interior Komplemen dan Komplemen Penutup
  Interior dari komplemen suatu himpunan sama dengan komplemen dari penutupnya: $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
• Penutup Komplemen dan Komplemen Interior
  Penutup komplemen suatu himpunan identik dengan komplemen interiornya: $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Catatan Tambahan

Berikut beberapa fakta pendukung yang sering muncul dalam analisis ruang topologis:

• Jika U terbuka dan U ⊆ A, maka U ⊆ Int(A)
  Setiap himpunan terbuka yang berada dalam \( A \) otomatis menjadi bagian dari interiornya. Interior adalah himpunan terbuka terbesar yang dapat dimuat dalam \( A \).
• Jika A ⊆ B, maka Int(A) ⊆ Int(B)
  Inklusi antarhimpunan dipertahankan oleh operasi interior: setiap himpunan terbuka dalam \( A \) juga termasuk dalam \( B \).
• A terbuka jika dan hanya jika A = Int(A)
  Suatu himpunan terbuka persis ketika ia sama dengan interiornya. Ini adalah karakterisasi standar dalam topologi.
• Menentukan interior menggunakan bahasa R
  Bahasa R menyediakan fasilitas komputasi yang sangat baik untuk mengevaluasi interior himpunan dalam konteks analitis maupun topologis.

Tinjauan ini memberikan dasar yang kuat untuk memahami bagaimana interior bekerja dalam berbagai struktur topologis.