Ruang topologi normal
Sebuah ruang topologi \( X \) disebut normal jika memenuhi dua syarat berikut:
- Setiap himpunan satu unsur bersifat tertutup
Artinya, untuk setiap titik \( x \in X \), himpunan \(\{x\}\) harus tertutup dalam topologi yang digunakan. - Dua himpunan tertutup yang saling lepas dapat dipisahkan oleh dua himpunan terbuka yang juga saling lepas
Jika \( A \) dan \( B \) adalah dua himpunan tertutup yang tidak beririsan, maka terdapat dua himpunan terbuka \( U \) dan \( V \) dengan:
- \( A \subset U \)
- \( B \subset V \)
- \( U \cap V = \emptyset \).
Normalitas memberikan kerangka yang jelas tentang bagaimana ruang topologi mampu memisahkan dua himpunan tertutup yang tidak saling beririsan. Dalam ruang normal, selalu tersedia lingkungan terbuka yang benar-benar terpisah untuk masing-masing himpunan tersebut. Ini adalah salah satu sifat penting dalam topologi karena menjadi dasar bagi banyak konstruksi fungsi kontinu.
Contoh
Ambil contoh ruang topologi \( X = \mathbb{R} \) dengan topologi standar yang dibangkitkan oleh interval terbuka. Misalnya kita pilih dua himpunan tertutup yang saling lepas:
- \( A = \{0\} \), sebuah himpunan satu titik.
- \( B = [2, 3] \), sebuah interval tertutup.
Keduanya tertutup dalam topologi standar dan jelas tidak beririsan.
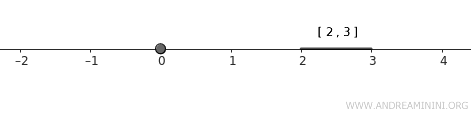
Catatan. Himpunan satu titik seperti \( A \) selalu tertutup. Interval seperti \( B \) juga tertutup, sehingga keduanya memenuhi sifat dasar ruang normal.
Untuk memisahkan keduanya menggunakan himpunan terbuka, kita dapat memilih:
Untuk \( A \): \( U = (-1, 1) \)
$$ A \subset U = (-1,1) $$
Untuk \( B \): \( V = (1, 4) \)
$$ B \subset V = (1,4) $$
Lingkungan terbuka ini tidak beririsan, sehingga memverifikasi bahwa garis bilangan real adalah ruang normal.
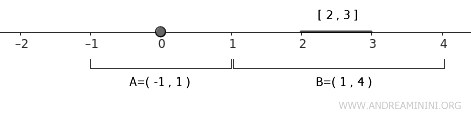
Kita bisa mengulangi proses yang sama untuk pasangan himpunan tertutup lain di \( \mathbb{R} \). Selama keduanya saling lepas, selalu ada lingkungan terbuka yang terpisah dengan jelas.
Catatan tambahan
Beberapa hal penting untuk diingat ketika membahas ruang normal:
- Topologi standar pada \( \mathbb{R} \) adalah contoh klasik ruang normal
Selain bersifat regular, \( \mathbb{R} \) juga memenuhi kondisi yang lebih kuat yaitu normalitas. - Semua ruang metrik bersifat normal
Karena struktur metrik menyediakan cara alami untuk menentukan jarak antara titik, pemisahan himpunan tertutup dengan lingkungan terbuka selalu dapat dilakukan. - Setiap ruang normal bersifat regular
Artinya normalitas mencakup regularitas sebagai sifat yang lebih lemah.
Sifat ini menjadi pondasi bagi banyak konsep lanjutan dalam topologi dan analisis, sehingga memahami ruang normal adalah langkah penting untuk memperdalam pemahaman mengenai struktur ruang topologis.