Topologi Subruang

Bayangkan kita memiliki ruang topologi \( (X, T) \), di mana \( X \) adalah sebuah himpunan dan \( T \) merupakan kumpulan himpunan-himpunan terbuka yang mendefinisikan topologi pada \( X \). Jika \( Y \) adalah himpunan bagian dari \( X \), maka topologi subruang pada \( Y \) didefinisikan sebagai koleksi: \[
T_Y = \{ U \cap Y \mid U \in T \}, \] artinya setiap himpunan terbuka di \( Y \) adalah hasil irisan antara suatu himpunan terbuka di \( X \) dan himpunan \( Y \). Topologi ini juga dikenal dengan sebutan topologi terinduksi.

Secara sederhana, suatu himpunan \( V \subseteq Y \) dikatakan terbuka dalam topologi subruang jika dapat ditulis sebagai hasil irisan antara \( Y \) dan himpunan terbuka \( U \) di ruang asal \( X \).

Jadi, semua himpunan terbuka dalam topologi subruang \( Y \) berbentuk \( U \cap Y \), dengan \( U \) terbuka di \( X \).

$$ V_{terbuka \ dalam \ Y} = U \cap Y $$

Begitu pula, semua himpunan tertutup dalam topologi subruang \( Y \) berbentuk \( C \cap Y \), dengan \( C \) tertutup di \( X \).

$$ V_{tertutup \ dalam \ Y} = C \cap Y $$

Dengan demikian, subruang topologis dapat dipahami sebagai himpunan bagian dari suatu ruang topologi yang dilengkapi dengan topologi yang diwarisi dari ruang asalnya.

Catatan. Himpunan terbuka dalam topologi subruang \( Y \) tidak selalu terbuka dalam ruang topologi \( X \). Ada kalanya suatu himpunan terbuka di \( Y \) justru tertutup di \( X \), atau sebaliknya. Bahkan, beberapa himpunan bisa terbuka dan tertutup sekaligus, disebut clopen. Pada contoh di bawah ini, kita akan melihat bagaimana hal tersebut terjadi.

Contoh Praktis

Pertimbangkan ruang topologi \( \mathbb{R} \) dengan topologi standar, di mana himpunan-himpunan terbukanya adalah interval terbuka.

Ambil \( Y = [0, 1] \) sebagai himpunan bagian dari \( \mathbb{R} \).

Topologi subruang pada \( Y \) mencakup semua himpunan berbentuk:

$$ U \cap [0, 1] $$

dengan \( U \) merupakan himpunan terbuka dalam \( \mathbb{R} \).

Sebagai contoh, interval (-1, 0.5) adalah himpunan terbuka dalam \( \mathbb{R} \).

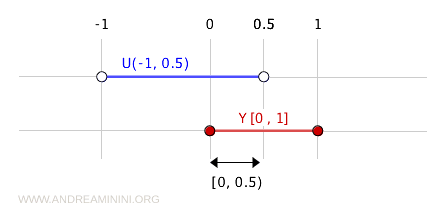
Irisan antara (-1, 0.5) dan \( Y = [0, 1] \) menghasilkan himpunan terbuka dalam topologi subruang \( Y \):

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Maka, interval \( [0, 0.5) \) terbuka dalam subruang \( Y \).

Sebaliknya, himpunan \( [0, 0.5] \) adalah tertutup dalam topologi subruang \( Y \) karena dapat diperoleh dari irisan antara himpunan tertutup [-1, 0.5] di \( X \) dengan \( Y \):

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Kesimpulannya, subruang topologi \( Y \) mewarisi struktur topologi dari \( X \): himpunan terbuka di \( Y \) adalah hasil irisan antara \( Y \) dan himpunan terbuka di \( X \).

Catatan. Himpunan seperti [0,a) atau (a,1], dengan 0<a<1, bersifat tertutup dalam topologi standar pada  $ \mathbb{R} $, tetapi terbuka dalam topologi subruang. Hal ini karena himpunan-himpunan tersebut dapat diperoleh sebagai hasil irisan antara Y=[0,1] dan himpunan terbuka dalam  $ \mathbb{R} $. Sebagai contoh: $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ Interval [0,0.5) terbuka dalam subruang Y meskipun tidak terbuka dalam topologi standar pada  $ \mathbb{R} $.

Ada himpunan yang terbuka di kedua ruang, seperti (0.2, 0.8), dan ada pula yang tertutup di keduanya, seperti [0.2, 0.8].

Dalam topologi subruang \( Y = [0, 1] \), himpunan \( [0, 1] \) bahkan bersifat terbuka dan tertutup sekaligus.

• Terbuka
  Untuk menunjukkan bahwa \( [0, 1] \) terbuka dalam subruang \( Y \), kita cukup menemukan himpunan terbuka \( U \) dalam \( \mathbb{R} \) sehingga \( U \cap Y = [0, 1] \). Jika kita ambil \( U = \mathbb{R} \), maka jelas: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Jadi, \( [0, 1] \) terbuka dalam subruang \( Y \).
• Tertutup
  Untuk membuktikan bahwa \( [0, 1] \) tertutup dalam subruang \( Y \), ambillah \( C = [0, 1] \), yang merupakan himpunan tertutup dalam \( \mathbb{R} \). Maka: $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Sehingga \( [0, 1] \) juga tertutup dalam subruang \( Y \).

  Catatan: Hal ini juga dapat dilihat dari komplemennya. Komplement dari \( [0, 1] \) dalam \( Y \) adalah himpunan kosong, yang selalu terbuka dalam topologi apa pun. Karena komplemen dari himpunan terbuka bersifat tertutup, maka \( [0, 1] \) tertutup dalam \( Y \).

Kesimpulannya, dalam topologi subruang \( Y = [0, 1] \), himpunan \( [0, 1] \) merupakan himpunan clopen, yaitu terbuka dan tertutup sekaligus.

Contoh 2

Pertimbangkan topologi standar pada himpunan bilangan real \(\mathbb{R}\).

Dalam topologi ini, setiap interval terbuka (a,b) dengan $ a > b $ adalah himpunan terbuka.

Salah satu contoh subruang topologis dari \(\mathbb{R}\) adalah himpunan bilangan bulat \(\mathbb{Z}\). Setiap bilangan bulat dapat diperoleh sebagai hasil irisan antara interval terbuka di \(\mathbb{R}\) dengan himpunan \(\mathbb{Z}\).

Sebagai contoh, bilangan 7 diperoleh dari:

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

Dengan cara yang sama, setiap bilangan bulat lainnya juga bisa diperoleh.

Artinya, setiap bilangan bulat merupakan himpunan terbuka dalam subruang topologi \(\mathbb{Z}\). Setiap himpunan bagian dari \(\mathbb{Z}\) juga bersifat terbuka dalam subruang ini.

Sebagai contoh, untuk memperoleh {6,7,8}, kita cukup mengiris himpunan terbuka (5.5,8.5) dengan \(\mathbb{Z}\):

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Subruang topologi pada \(\mathbb{Z}\) ini dikenal sebagai topologi diskret.

Catatan: Topologi diskret pada \(\mathbb{Z}\) bukanlah subruang dari topologi standar pada \(\mathbb{R}\), melainkan topologi yang berdiri sendiri. Namun, topologi subruang yang diwarisi \(\mathbb{Z}\) dari topologi standar pada \(\mathbb{R}\) ternyata identik dengan topologi diskret pada \(\mathbb{Z}\).

Contoh 3

Pertimbangkan ruang Euclidean tiga dimensi \(\mathbb{R}^3\) dengan topologi standar, di mana himpunan-himpunan terbukanya merupakan gabungan dari bola-bola terbuka.

Sekarang perhatikan bola satuan \( S^2 \), yaitu himpunan semua titik di \(\mathbb{R}^3\) yang berjarak tepat 1 dari titik asal:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

Topologi subruang pada \( S^2 \) didefinisikan sebagai:

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ terbuka dalam } \mathbb{R}^3 \} $$

Artinya, suatu himpunan \( V \subseteq S^2 \) terbuka dalam topologi subruang jika dan hanya jika dapat ditulis sebagai hasil irisan antara \( S^2 \) dan himpunan terbuka \( U \) dalam \(\mathbb{R}^3\).

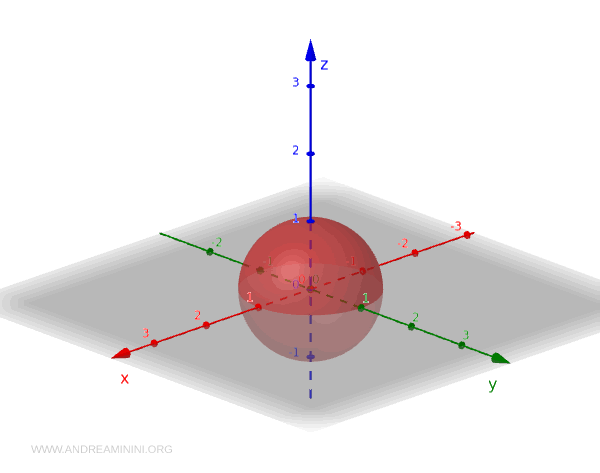
Berikut beberapa contoh himpunan terbuka dalam \( S^2 \):

• Gabungan subruang terbuka di \(\mathbb{R}^3\)
  Misalkan \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} \). Irisan antara \( U \) dan \( S^2 \) adalah: $$ U \cap S^2 = S^2 $$ karena setiap titik di \( S^2 \) memenuhi \( x^2 + y^2 + z^2 = 1 \), yang jelas lebih kecil dari 2. Jadi, \( S^2 \) bersifat terbuka terhadap dirinya sendiri.
• Bagian atas permukaan bola
  Misalkan \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid z > 0 \} \). Himpunan ini mewakili setengah bagian atas bola satuan. Irisan dengan \( S^2 \) menghasilkan: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Himpunan ini menggambarkan permukaan atas bola dan merupakan himpunan terbuka dalam topologi subruang \( T_{S^2} \).
• Himpunan terbuka dan sifat-sifatnya
  Himpunan kosong \( \emptyset \) dan bola satuan \( S^2 \) sendiri selalu terbuka dalam \( S^2 \).
  
  • Irisan berhingga dari himpunan terbuka di \( S^2 \) tetap terbuka dalam \( S^2 \).
  • Gabungan sebarang banyak himpunan terbuka di \( S^2 \) juga terbuka dalam \( S^2 \).

Kesimpulannya, bola satuan \( S^2 \) sebagai subruang topologis dari \(\mathbb{R}^3\) mewarisi struktur topologi dari topologi standar ruang tiga dimensi tersebut. Setiap himpunan terbuka di \( S^2 \) merupakan hasil irisan antara \( S^2 \) dan himpunan terbuka dalam \(\mathbb{R}^3\).

Sifat-Sifat Topologi Subruang

Topologi subruang memiliki sejumlah sifat penting yang membantu memahami bagaimana topologi ruang asal diturunkan ke bagian-bagiannya:

1. Himpunan terbuka
   Semua himpunan terbuka dalam \( Y \) berbentuk \( U \cap Y \), dengan \( U \) terbuka dalam \( X \).
2. Himpunan kosong dan himpunan penuh
   Himpunan kosong \( \emptyset \) dan himpunan \( Y \) sendiri selalu terbuka dalam \( Y \):
   - \( \emptyset \) terbuka karena \( \emptyset = \emptyset \cap Y \).
   - \( Y \) terbuka karena \( Y = X \cap Y \).
3. Irisan berhingga
   Irisan dari sejumlah berhingga himpunan terbuka dalam \( Y \) tetap terbuka dalam \( Y \). Jika \( V_1, \ldots, V_n \) terbuka dalam \( Y \), maka: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap Y) \cap \cdots \cap (U_n \cap Y) = (U_1 \cap \cdots \cap U_n) \cap Y $$ karena irisan berhingga dari himpunan terbuka di \( X \) juga terbuka.
4. Gabungan sebarang banyak
   Gabungan dari himpunan-himpunan terbuka dalam \( Y \) juga terbuka dalam \( Y \). Jika setiap \( V_\alpha \) terbuka dalam \( Y \), maka: $$ \bigcup_{\alpha \in I} V_\alpha = \bigcup_{\alpha \in I} (U_\alpha \cap Y) = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$ karena gabungan sebarang banyak himpunan terbuka dalam \( X \) tetap terbuka.

Catatan Tambahan

Beberapa poin penting untuk dipahami tentang topologi subruang:

• Topologi standar pada setiap subruang \( Y \) dari \(\mathbb{R^n}\) identik dengan topologi subruang yang diperoleh dari \(\mathbb{R^n}\).

  Contoh. Misalkan Y = [-1,0) ∪ (0,1], yang merupakan himpunan bagian dari \( \mathbb{R} \). Dalam topologi standar pada Y, interval [-1,0) dan (0,1] keduanya terbuka karena dapat diperoleh sebagai hasil irisan antara Y dan himpunan terbuka pada \( \mathbb{R} \). Misalnya, ambil himpunan terbuka (-1.5,0.5) dan (0,1.5) di \( \mathbb{R} \): $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Maka, topologi standar pada Y identik dengan topologi subruang yang diturunkan dari topologi standar pada \( \mathbb{R} \). Dalam hal ini, interval [-1,0) dan (0,1] juga tertutup dalam topologi standar pada Y, karena komplemen dari [-1,0) adalah (0,1], dan sebaliknya. Jadi, kedua interval tersebut merupakan himpunan "clopen", yaitu terbuka dan tertutup sekaligus.

• Teorema Basis dalam Topologi Subruang
  Teorema ini menjelaskan bahwa jika kita memiliki basis $ B_X $ untuk topologi ruang topologi \( X \), dan kita ambil himpunan bagian \( Y \subset X \), maka himpunan-himpunan yang terbentuk dari irisan antara elemen basis \( B_X \) dengan \( Y \) membentuk basis $ B_Y $ untuk topologi subruang pada \( Y \). $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$

Dengan cara ini, konsep topologi subruang membantu kita memahami bagaimana sifat-sifat topologi suatu ruang dapat "diturunkan" ke dalam bagian-bagian tertentu darinya, tanpa kehilangan konsistensi dengan struktur topologi ruang asal.