Basis dalam Topologi

Basis topologi adalah kumpulan himpunan terbuka, disebut B, di mana setiap himpunan terbuka dalam ruang topologi T dapat dibentuk dari gabungan himpunan-himpunan dalam B.

Jika kita memiliki himpunan X dan himpunan bagian T dari X yang mendefinisikan suatu topologi pada X, maka basis dari topologi T adalah himpunan B yang berisi himpunan-himpunan yang disebut elemen dasar. Basis ini harus memenuhi dua syarat penting:

• Setiap elemen x dalam X harus termasuk ke dalam setidaknya satu himpunan di B.
• Jika suatu elemen x berada dalam irisan tak kosong antara dua himpunan B₁ dan B₂ dalam B, maka harus ada himpunan B₃ di dalam irisan tersebut yang juga memuat x.
  

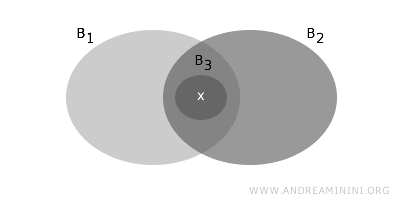
Dua syarat ini memastikan bahwa himpunan B benar-benar berfungsi sebagai dasar pembentuk topologi T.

Mengapa hal ini penting?

Basis membantu kita membangun topologi T dari gabungan elemen-elemen dasarnya, tanpa perlu menuliskan semua himpunan terbuka satu per satu. Dengan cara ini, struktur topologi dapat dijelaskan secara ringkas namun lengkap.

Catatan. Syarat mengenai irisan antar elemen dasar menjamin bahwa topologi tetap konsisten dengan aksioma dasar, misalnya bahwa irisan dua himpunan terbuka juga merupakan himpunan terbuka.

Contoh Praktis

Pertimbangkan himpunan X berikut:

$$ \{a, b, c \} $$

dan topologi T berikut:

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Pada kasus ini, T memuat seluruh himpunan terbuka dalam X. Setiap elemen T adalah himpunan terbuka menurut definisi topologi.

Salah satu basis B yang sesuai untuk topologi ini adalah:

$$ B = \{ \{ a \} ,\{ b,c \} \} $$

Basis ini memenuhi semua syarat, karena setiap elemen dalam X={a,b,c} berada di dalam salah satu himpunan di B, dan tidak ada irisan yang bertentangan.

Dengan demikian, setiap himpunan terbuka dalam T dapat dinyatakan sebagai gabungan dari himpunan-himpunan dalam B.

Misalnya, himpunan {a} sudah termasuk dalam B, {b,c} juga termasuk dalam B, dan seluruh ruang X dapat dibentuk dari gabungan keduanya:

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Catatan. Dalam teori himpunan, himpunan kosong  Ø  adalah himpunan bagian tidak tepat dari setiap himpunan dan selalu dianggap termasuk secara definisi. Karena itu, himpunan kosong juga termasuk dalam B. $$ \emptyset \in B $$ Selain itu, himpunan kosong selalu merupakan himpunan terbuka dalam setiap topologi.

Contoh ini memperlihatkan bagaimana konsep himpunan terbuka bekerja pada ruang berhingga. Dalam ruang yang lebih kompleks atau tak hingga, ide dasarnya tetap sama: basis memberikan "blok pembentuk" untuk semua himpunan terbuka dalam ruang topologi.

Pendekatan Alternatif

Basis lain untuk topologi pada himpunan X={a,b,c} dapat ditulis sebagai:

$$ B = \{ \{ a \} ,\{ b \}, \{ c \} \} $$

Di sini, basis terdiri atas himpunan-himpunan tunggal dari setiap elemen X.

Hal ini menunjukkan bahwa B juga membentuk basis bagi topologi T={ Ø,X,{a},{b,c}}.

• Himpunan kosong Ø adalah himpunan terbuka secara definisi dan selalu disertakan.
• Himpunan {a} sudah terdapat dalam B. $$ \{ a \} \in B $$
• Himpunan {b,c} dapat dibentuk dari gabungan {b} dan {c}, keduanya termasuk dalam B. $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• Seluruh himpunan X={a,b,c} dapat diperoleh dari gabungan semua himpunan dalam B: $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

Dengan demikian, B tetap berfungsi sebagai basis untuk topologi pada X karena memungkinkan kita membentuk semua himpunan terbuka dalam T melalui gabungan himpunan-himpunan di B.

Catatan. Contoh ini menunjukkan bahwa satu topologi bisa memiliki beberapa basis yang berbeda, masing-masing memberikan cara tersendiri untuk "menghasilkan" himpunan-himpunan terbuka melalui gabungan elemen dasar.

Contoh 2

Pertimbangkan himpunan semua interval bilangan real (a,b) dengan a<b. Himpunan ini mencakup seluruh garis bilangan real:

$$ B=\{ \ (a,b) ⊂ \ R \ | \ a < b \ \} $$

Himpunan tersebut merupakan basis karena setiap titik pada garis real selalu berada di dalam suatu interval terbuka (a,b).

Selain itu, jika dua interval terbuka beririsan, maka titik di dalam irisan tersebut juga termasuk dalam interval lain yang merupakan bagian dari B dan berada di dalam irisan itu.

Sebagai contoh, untuk dua interval terbuka (0, 3) dan (2, 4), irisan keduanya adalah (2,3).

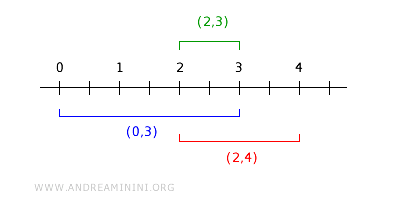
Interval (2,3) ini merupakan salah satu himpunan B_i dalam basis B dan berada di dalam irisan tersebut. $$ (0,3) \cap (2,4) = (2,3) ∈  B_i ⊂ (0,3) \cap (2,4) ⊂ B $$

Basis Terhitung dalam Topologi

Basis terhitung dalam topologi adalah kumpulan terhitung dari himpunan-himpunan terbuka \( \mathcal{B} = \{B_1, B_2, B_3, \dots\} \), di mana setiap himpunan terbuka dalam ruang \( X \) dapat dibentuk sebagai gabungan dari elemen-elemen di dalam \( \mathcal{B} \).

Suatu himpunan disebut terhitung apabila jumlah elemennya hingga, atau jika setiap elemennya dapat dipasangkan satu per satu dengan bilangan asli \( \mathbb{N} \).

Dengan kata lain, suatu koleksi dikatakan terhitung jika setiap elemen dapat diberi penomoran seperti \( B_1, B_2, B_3, \dots \).

Perbedaan antara Basis dan Basis Terhitung

Pada dasarnya, setiap basis mampu membangkitkan topologi. Namun, hanya basis yang terdiri atas jumlah himpunan terbuka yang terbatas secara terhitung yang disebut basis terhitung. Artinya, meskipun bisa saja ada tak terhingga banyaknya himpunan dalam basis, semuanya tetap dapat diurutkan satu per satu.

Mengapa ini penting? Basis terhitung memiliki peran penting dalam banyak cabang topologi dan analisis. Misalnya, keberadaan basis terhitung merupakan salah satu syarat dalam Teorema Metrisasi Urysohn. Selain itu, banyak hasil teoretis yang menjadi lebih sederhana atau hanya berlaku dalam ruang dengan basis terhitung.

Contoh

Pertimbangkan ruang \( \mathbb{R} \) dengan topologi standar. Kumpulan semua interval terbuka \( (a, b) \) dengan \( a, b \in \mathbb{Q} \) (bilangan rasional) dan \( a < b \) merupakan contoh basis terhitung.

Kita dapat menyusun semua interval tersebut secara berurutan, misalnya dengan memberi label I₁, I₂, I₃, dan seterusnya. Inilah yang membuatnya terhitung.

Pembuktian

Himpunan bilangan asli bersifat terhitung karena dapat disusun dalam urutan berikut:

\[ 1,\ 2,\ 3,\ 4,\ 5,\ \dots \]

Jika semua interval \( (a, b) \) dengan ujung-ujung rasional \( a < b \) dapat disusun dengan cara yang sama, maka kumpulan interval tersebut juga terhitung.

Walaupun bilangan rasional jumlahnya tak hingga, ia tetap terhitung. Misalnya, bilangan rasional dapat diurutkan seperti ini:

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

Misalkan urutan ini kita tulis sebagai \( q_1, q_2, q_3, \dots \). Selanjutnya, pertimbangkan semua pasangan \( (q_i, q_j) \) yang memenuhi \( q_i < q_j \).

Beberapa contohnya adalah:

• \( (q_1, q_2) = (0, 1) \)
• \( (q_3, q_2) = (-1, 1) \)
• \( (q_4, q_5) = (\tfrac{1}{2}, -\tfrac{1}{2}) \) ❌ tidak valid karena \( a > b \)
• \( (q_5, q_1) = (-\tfrac{1}{2}, 0) \)

Setiap pasangan valid (yakni dengan \( a < b \)) mendefinisikan sebuah interval terbuka yang unik.

Karena itu, kita dapat menyusunnya dalam urutan:

1. \( (0, 1) \)
2. \( (-1, 1) \)
3. \( (-\tfrac{1}{2}, 0) \)
4. \( (0, \tfrac{1}{2}) \)
5. \( (-1, \tfrac{1}{2}) \)
6. \( (\tfrac{1}{2}, 1) \)
7. \( (-\tfrac{2}{3}, 0) \)
8. \( (0, \tfrac{2}{3}) \)
9. \( (-1, \tfrac{2}{3}) \)
10. \( (-\tfrac{1}{2}, \tfrac{1}{2}) \)

Meskipun jumlahnya tak hingga, kita dapat menyusunnya secara berurutan seperti bilangan asli. Itulah yang dimaksud dengan himpunan terhitung.

Dengan demikian, kumpulan semua interval \( (a, b) \) dengan ujung rasional dan \( a < b \) bersifat terhitung, karena dapat diurutkan seluruhnya tanpa ada yang terlewat - sama seperti urutan 1, 2, 3, dan seterusnya.

Catatan Tambahan

Berikut beberapa pengamatan menarik tentang konsep basis dalam topologi:

• Jika kita memiliki himpunan X dan membentuk basis B sedemikian rupa sehingga setiap elemen x∈X direpresentasikan sebagai himpunan {x}∈B, maka basis ini dapat digunakan untuk membangun berbagai topologi pada X.

  Dengan mengambil gabungan dari himpunan-himpunan tunggal tersebut, kita dapat menghasilkan beragam struktur topologi yang berbeda.
  
  Misalnya, basis B={ {a}, {b}, {c} } pada himpunan X={a,b,c} dapat membangkitkan topologi T={Ø,{a},{b,c},X}.
  
  Basis yang sama juga dapat digunakan untuk membentuk topologi lain, seperti T={Ø,{b},{a,c},X}, topologi trivial T={Ø, X}, atau topologi diskrit T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X}.

  Catatan. Syarat pertama terpenuhi karena setiap elemen X terdapat dalam salah satu himpunan di B. Syarat kedua juga terpenuhi karena setiap {x} bersifat saling lepas (disjoint), masing-masing hanya berisi satu elemen dari X.

Contoh ini memperlihatkan bagaimana basis dapat digunakan untuk membangun berbagai topologi yang berbeda, dan betapa pentingnya konsep basis terhitung dalam memahami struktur dasar ruang topologi.