Gabungan Interior Dua Himpunan
Gabungan interior dua himpunan $ A $ dan $ B $ selalu termasuk dalam interior gabungan keduanya. \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Namun, kesetaraan tidak selalu terjadi.
Gagasan ini memberikan gambaran penting dalam topologi. Interior setiap himpunan bersifat "aman" di dalam interior gabungan, tetapi keduanya tidak selalu menghasilkan himpunan yang sama. Dalam banyak kasus, gabungan interior hanya menjadi bagian dari interior gabungan.
Contoh Praktis untuk Memahami Idenya
Pertimbangkan dua interval terbuka di \(\mathbb{R}\):
$$ A = (0, 2) $$ $$ B = (1, 3) $$
Keduanya terbuka, sehingga interiornya sama dengan interval itu sendiri:
$$ \text{Int}(A) = (0, 2) $$ $$ \text{Int}(B) = (1, 3) $$
Gabungan interior memberi kita:
$$ (0, 2) \cup (1, 3) $$
Kedua interval saling tumpang tindih, sehingga gabungannya menjadi:
$$ (0, 3) $$
Interior gabungan juga:
$$ \text{Int}(A \cup B) = (0, 3) $$
Pada contoh ini, gabungan interior dan interior gabungan ternyata sama. Namun hal ini tidak selalu berlaku, terutama jika himpunan tidak tumpang tindih secara penuh.
Contoh Saat Kesetaraan Gagal
Misalkan $$ A = [0, 2] $$ dan $$ B = [2, 3] $$ Interiornya adalah $$ (0, 2) $$ dan $$ (2, 3) $$. Gabungan keduanya adalah $$ [0, 3] $$ dan interior gabungan adalah $$ (0, 3) $$. Maka $$ (0, 2) \cup (2, 3) \subseteq (0, 3) $$. Namun titik 2 berada di interior gabungan, tetapi tidak berada di interior salah satu himpunan awal. Karena itu kedua himpunan tidak sama.
Contoh ini menunjukkan dengan jelas bahwa gabungan interior memang selalu termasuk dalam interior gabungan, meskipun tidak selalu identik.
Contoh Interval Terpisah
Ambil dua interval terbuka yang tidak saling bersentuhan:
$$ A = (0, 1) $$ $$ B = (2, 3) $$
Interior masing-masing sama dengan interval itu sendiri, dan baik gabungan interior maupun interior gabungan menghasilkan:
$$ (0, 1) \cup (2, 3) $$
Pada kasus ini, kesetaraan kembali terjadi karena tidak ada bagian yang saling tumpang tindih.
Contoh di Bidang Dua Dimensi
Pertimbangkan dua cakram terbuka di \(\mathbb{R}^2\) yang saling tumpang tindih sebagian, masing-masing berpusat di \( (0, 0) \) dan \( (0.5, 0) \), dengan radius 1. Keduanya terbuka, sehingga interiornya sama dengan himpunannya sendiri.
Gabungan interior sama dengan gabungan kedua cakram:
$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$
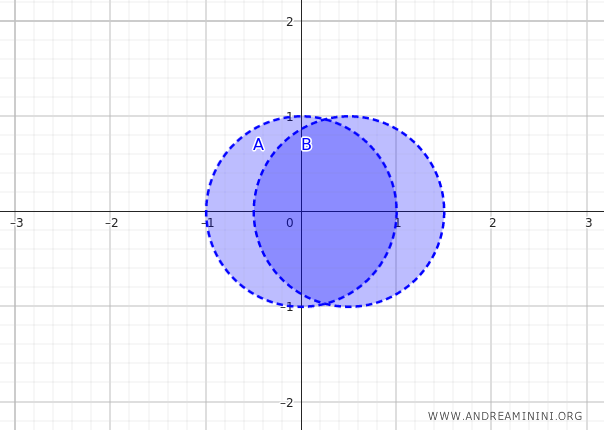
Interior gabungan juga mencakup keseluruhan wilayah tersebut. Ini kembali memperkuat bahwa gabungan interior memang berada dalam interior gabungan.
Pembuktian Inti
Untuk memahami alasannya, mulai dari definisi interior. Titik berada di interior suatu himpunan jika ia memiliki lingkungan kecil yang sepenuhnya berada dalam himpunan itu.
Jika suatu titik berada di dalam \(\text{Int}(A)\) atau \(\text{Int}(B)\), maka titik tersebut memiliki lingkungan yang berada dalam \( A \) atau \( B \). Lingkungan ini otomatis berada dalam gabungan \( A \cup B \), sehingga titik tersebut merupakan titik interior dari gabungan itu.
Dari sini dapat disimpulkan bahwa:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Ini adalah alasan mendasar mengapa sifat tersebut selalu berlaku, baik pada interval sederhana maupun himpunan yang lebih kompleks.