Topologi Persegi Panjang Terbuka
Topologi persegi panjang terbuka merupakan salah satu konsep dasar dalam studi topologi pada bidang R2. Dalam pendekatan ini, himpunan terbuka didefinisikan sebagai gabungan dari persegi panjang terbuka. Setiap persegi panjang terbuka adalah hasil kali Kartesius dari dua selang terbuka di sepanjang sumbu koordinat, membentuk kerangka yang membantu kita memahami struktur ruang dua dimensi secara lebih intuitif.
Topologi ini dibangun di atas sebuah basis yang terdiri sepenuhnya dari lingkungan persegi panjang terbuka. Bentuk-bentuk inilah yang menjadi komponen dasar untuk membangun struktur ruang yang lebih kompleks dan menjadi cara alternatif untuk memandang bagaimana titik-titik saling berhubungan di bidang Euclidean.
Secara sederhana, suatu himpunan \( U \subseteq \mathbb{R}^2 \) dikatakan terbuka jika untuk setiap titik \( (x, y) \) di dalamnya terdapat sebuah persegi panjang terbuka yang memuat titik tersebut dan seluruhnya berada di dalam \( U \). Dengan kata lain, di sekitar setiap titik dalam \( U \), selalu ada ruang kecil berbentuk persegi panjang yang masih termasuk dalam himpunan itu.
Persegi panjang terbuka ini menjadi elemen kunci yang menyusun topologi bidang Euclidean.
$$ B = \{ (a, b) \times (c, d) \ | \ a<b, \ c<d \} $$
Dalam hal ini, \( a, b, c, d \) adalah bilangan real dengan \( a < b \) dan \( c < d \), yang menentukan batas-batas selang di sepanjang sumbu \( x \) dan \( y \).
Pendekatan ini memberikan perspektif alternatif terhadap topologi Euclidean standar, yang biasanya dijelaskan menggunakan lingkungan berbentuk lingkaran di sekitar titik-titik pada bidang.
Catatan: Pendekatan ini menunjukkan betapa fleksibelnya konsep dasar topologi. Baik menggunakan lingkaran maupun persegi panjang, kita tetap bisa membentuk basis topologi yang sama. Bentuknya mungkin berbeda, tetapi definisi himpunan terbuka dan struktur ruang yang dihasilkan tetap setara.
Contoh Persegi Panjang Terbuka
Untuk memahami ide ini dengan lebih jelas, mari kita lihat contoh konkret. Sebuah persegi panjang terbuka pada bidang \( \mathbb{R}^2 \) dapat dianggap sebagai hasil kali Kartesius dari dua selang terbuka, satu di sepanjang sumbu \( x \) dan satu di sepanjang sumbu \( y \).
Misalnya, pertimbangkan selang terbuka \( (1, 3) \) pada sumbu \( x \) dan \( (2, 4) \) pada sumbu \( y \).
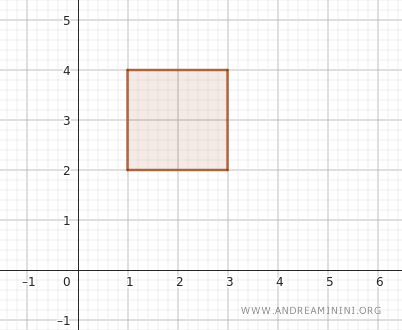
Dari kedua selang ini terbentuk persegi panjang terbuka yang memuat semua titik \( (x, y) \) dengan \( x \) berada antara 1 dan 3, serta \( y \) berada antara 2 dan 4.
Secara formal, persegi panjang tersebut dinyatakan sebagai \( (1, 3) \times (2, 4) \).
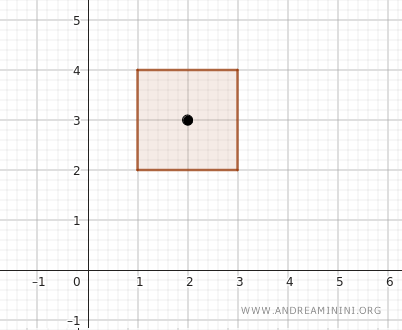
Jika kita ambil satu titik di dalamnya, misalnya \( (2, 3) \), titik ini memenuhi syarat karena koordinat \( x \)-nya lebih besar dari 1 dan kurang dari 3, sedangkan koordinat \( y \)-nya lebih besar dari 2 dan kurang dari 4. Dengan kata lain, titik ini benar-benar berada di dalam persegi panjang terbuka.
Catatan: Perlu diingat bahwa tepi persegi panjang tidak termasuk dalam himpunan terbuka. Jadi titik-titik seperti \( (1, y) \), \( (3, y) \), \( (x, 2) \), atau \( (x, 4) \) berada di luar persegi panjang tersebut.