Penutupan suatu himpunan
Penutupan suatu himpunan \( A \) dalam sebuah ruang topologi \( X \) didefinisikan sebagai irisan dari semua himpunan tertutup yang memuat \( A \). Irisan ini dilambangkan dengan \( \text{Cl}(A) \).
Dengan kata lain, penutupan himpunan A adalah himpunan tertutup paling kecil yang sepenuhnya mencakup A.
Tidak ada himpunan tertutup lain yang memuat A dengan ukuran yang lebih kecil daripada penutupannya.
Catatan: Pernyataan ini langsung mengikuti definisi penutupan, yaitu sebagai irisan dari seluruh himpunan tertutup yang memuat A. Secara intuitif, penutupan dapat dipahami sebagai “batas tertutup” paling rapat yang mengelilingi A, yang terdiri atas elemen-elemen yang selalu muncul di setiap himpunan tertutup yang mencakup A.
Secara formal, penutupan himpunan A dituliskan sebagai:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ dan } C \text{ tertutup di } X \} $$
Di sini, \( \text{Cl}(A) \) menyatakan penutupan dari \( A \), sedangkan simbol \( \bigcap \) menyatakan irisan dari semua himpunan tertutup \( C \) yang memuat \( A \).
Penutupan \( A \) mencakup himpunan \( A \) itu sendiri beserta seluruh titik batasnya di dalam ruang \( X \).
Catatan: Perlu diperhatikan bahwa penutupan suatu himpunan \( A \) terutama ditentukan oleh topologi ruang \( X \) tempat \( A \) berada, bukan oleh sifat internal himpunan \( A \) itu sendiri. Oleh karena itu, himpunan yang sama dapat memiliki penutupan yang berbeda jika topologi ruangnya berbeda.
Contoh ilustratif
Ambil himpunan \( A = (0, 1) \) di dalam bilangan real \( \mathbb{R} \) dengan topologi standar.
Himpunan ini adalah interval terbuka yang memuat semua bilangan real antara 0 dan 1, tanpa menyertakan kedua titik ujungnya.
Dalam konteks ini, penutupan dari \( A \) adalah:
$$ \text{Cl}(A) = [0,1] $$
Himpunan ini mencakup interval terbuka awal \( (0,1) \) sekaligus titik-titik batasnya, yaitu 0 dan 1.
Catatan: Dalam topologi standar pada \( \mathbb{R} \), suatu himpunan disebut tertutup jika memuat semua titik batasnya. Titik batas adalah titik yang setiap lingkungannya selalu mengandung titik lain dari himpunan tersebut. Sebagai contoh, irisan interval tertutup [0,2] dan [-1,1] menghasilkan [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$ Tidak ada interval tertutup yang lebih kecil yang dapat memuat (0,1).
Contoh 2
Selanjutnya, perhatikan himpunan \( A = [0, 1) \) di dalam \( \mathbb{R} \) dengan topologi standar.
Himpunan ini memuat semua bilangan real dari 0 hingga mendekati 1, dengan 0 termasuk dan 1 tidak termasuk. Karena itu, himpunan ini merupakan interval tertutup di kiri dan terbuka di kanan.
trPenutupan himpunan ini kembali diperoleh sebagai:
$$ \text{Cl}(A) = [0,1] $$
Hal ini terjadi karena titik 0 sudah termasuk di dalam A, sedangkan titik 1 merupakan titik batas yang belum tercakup.
Dengan demikian, penutupan A menambahkan titik ujung kanan interval, sehingga [0,1] menjadi himpunan tertutup paling kecil yang memuat A.
Catatan: Prinsip ini konsisten dengan konsep penutupan dalam topologi, yang selalu mencakup seluruh titik akumulasi suatu himpunan. Sebagai ilustrasi, irisan dari [0,2] dan [-1,1] adalah [0,1]. $$ [0,2] \cap [-1,1]=[0,1] $$
Contoh 3
Sekarang, kita tinjau kembali himpunan yang sama \( A = [0,1) \), tetapi kali ini ruang \( X \) dilengkapi dengan topologi diskret.
Dalam topologi diskret, setiap subhimpunan dari ruang topologi bersifat terbuka sekaligus tertutup.
- Himpunan terbuka
Karena setiap subhimpunan dari \( X \) bersifat terbuka, maka \( A \subset X \) secara langsung merupakan himpunan terbuka. - Himpunan tertutup
Setiap subhimpunan juga bersifat tertutup karena komplemennya merupakan himpunan terbuka. Sebagai contoh, komplemen \( X/A \) adalah subhimpunan dari X, sehingga bersifat terbuka. Oleh karena itu, A juga tertutup.
Kondisi ini menunjukkan bahwa setiap himpunan dalam topologi diskret bersifat sekaligus terbuka dan tertutup, yang dikenal sebagai himpunan clopen.
Akibatnya, penutupan dari \( A \) tidak menambahkan elemen apa pun:
$$ \text{Cl}(A) = [0,1) $$
Himpunan tertutup paling kecil yang memuat \( A \) adalah \( A \) itu sendiri.
Catatan: Contoh ini menegaskan bahwa pilihan topologi sangat memengaruhi penutupan suatu himpunan. Sifat tertutup bukanlah karakteristik mutlak dari himpunan \( A \), melainkan bergantung pada struktur topologi ruang \( X \).
Contoh 4
Misalkan ruang topologi \( X \) terdiri atas titik-titik \( \{a, b, c\} \) dan dilengkapi dengan topologi diskret.
Dalam topologi diskret, setiap subhimpunan dari \( X \) bersifat terbuka:
- \( \emptyset \) dan \( \{a, b, c\} \) terbuka secara definisi.
- Setiap himpunan satu elemen, yaitu \( \{a\} \), \( \{b\} \), dan \( \{c\} \), merupakan himpunan terbuka.
- Setiap kombinasi dari elemen-elemen tersebut, seperti \( \{a, b\} \), \( \{a, c\} \), dan \( \{b, c\} \), juga bersifat terbuka.
Selain itu, karena komplemen dari setiap subhimpunan juga terbuka, maka semua subhimpunan dalam topologi diskret bersifat tertutup.
Artinya, dalam topologi diskret, setiap himpunan bersifat terbuka dan tertutup sekaligus.
Untuk himpunan \( A = \{b, c\} \), sifat ini berarti bahwa A sudah tertutup tanpa perlu penambahan elemen apa pun.
Penutupannya adalah:
\[ Cl(A) = \{b, c\} \]
Dalam topologi ini, konsep penutupan menjadi sangat sederhana karena setiap himpunan sudah “lengkap” sejak awal.
Catatan: Sebagai pemeriksaan cepat, himpunan tertutup yang memuat \( A \) adalah \( \{b, c\} \) dan \( \{a,b,c\} \). Irisannya adalah $$ Cl(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ yang persis sama dengan \( A \). Dengan demikian, benar bahwa \( Cl(A) = A \).
Teorema Penutupan Suatu Himpunan
Dalam sebuah ruang topologi \( X \), suatu elemen \( y \) termasuk dalam penutupan subhimpunan \( S \), yang dinotasikan dengan \( \text{Cl}(S) \), jika dan hanya jika setiap himpunan terbuka \( U \) yang memuat \( y \) selalu beririsan tidak kosong dengan \( S \): \( y \in \text{Cl}(S) \iff \forall \ U \text{ terbuka dengan } y \in U, \ U \cap S \neq \emptyset \).
Secara intuitif, sebuah titik \( y \) berada dalam penutupan \( S \) apabila tidak mungkin membangun himpunan terbuka di sekitar \( y \) tanpa "menyentuh" \( S \).
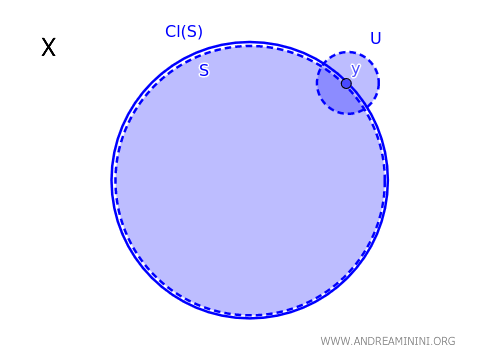
Teorema ini memberikan kriteria yang sederhana namun sangat kuat untuk mengenali apakah suatu titik merupakan bagian dari penutupan sebuah himpunan dalam ruang topologi.
Bukti
- Syarat perlu: Jika \( y \) termasuk dalam penutupan \( S \), maka berdasarkan definisinya setiap himpunan terbuka yang memuat \( y \) harus beririsan dengan \( S \). Hal ini mencerminkan hakikat penutupan, yang mencakup elemen-elemen himpunan sekaligus semua titik limitnya. Sebuah titik limit menuntut bahwa setiap lingkungan terbuka yang memuatnya selalu beririsan dengan himpunan asal.
- Syarat cukup: Sebaliknya, jika setiap himpunan terbuka yang memuat \( y \) selalu beririsan dengan \( S \), maka \( y \) merupakan titik limit dari \( S \) atau memang merupakan elemen dari \( S \) itu sendiri. Dengan demikian, \( y \) pasti termasuk dalam penutupan \( S \). Artinya, titik \( y \) dapat didekati sedekat mungkin oleh titik-titik dari \( S \).
Catatan: Teorema ini sangat penting dalam topologi karena menghubungkan konsep himpunan terbuka dengan penutupan himpunan. Hubungan ini menjadi dasar dalam pembahasan kekontinuan, kekonvergenan barisan, serta berbagai hasil penting lainnya dalam topologi.
Contoh
Pertimbangkan himpunan \( A = (0, 2) \) dalam topologi standar pada \( \mathbb{R} \). Himpunan ini merupakan interval terbuka pada garis bilangan real.
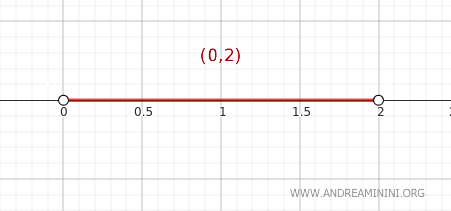
Kita akan menggunakan teorema penutupan untuk menentukan apakah suatu titik \( y \) termasuk dalam \( \text{Cl}(A) \), yaitu penutupan dari himpunan A.
Ambil titik \( y = 2 \).
Menurut teorema, \( y \in \text{Cl}(A) \) jika dan hanya jika setiap himpunan terbuka \( U \) yang memuat \( y \) beririsan dengan \( A \).
- Meninjau himpunan terbuka di sekitar \( y \): Setiap himpunan terbuka \( U \) yang memuat titik \( y = 2 \), seperti \( (1.9, 2.1) \), \( (1.95, 2.05) \), atau \( (1.99, 2.01) \), selalu mengandung titik-titik yang juga berada dalam interval \( A = (0, 2) \). Titik-titik seperti \( 1.95 \) dan \( 1.99 \) jelas terletak di antara 0 dan 2.
- Kesimpulan: Karena setiap himpunan terbuka di sekitar \( y = 2 \) selalu beririsan dengan \( A \), maka berdasarkan teorema penutupan dapat disimpulkan bahwa \( y = 2 \) termasuk dalam \( \text{Cl}(A) \).
Dengan demikian, titik \( y = 2 \) memang berada dalam penutupan \( A \).
$$ y \in \text{Cl}(A) $$
Hal ini konsisten dengan fakta bahwa penutupan dari himpunan \( A \) adalah interval tertutup \( \text{Cl}(A) = [0, 2] \), yang secara alami mencakup titik \( y = 2 \).
Sifat-sifat Penutupan dalam Ruang Topologi
Berikut ini beberapa sifat dasar penutupan suatu himpunan dalam ruang topologi, beserta relasinya dengan operasi lain seperti interior.
- Interior dari komplemen dan komplemen dari penutupan
Interior dari komplemen suatu himpunan \( A \) sama dengan komplemen dari penutupan \( A \): $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$ - Penutupan dari komplemen dan komplemen dari interior
Penutupan dari komplemen suatu himpunan \( A \) sama dengan komplemen dari interior \( A \): $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$
Pengamatan Penting
Beberapa pengamatan berikut merangkum sifat-sifat kunci penutupan himpunan dalam topologi.
- Jika C adalah himpunan tertutup di X dan A ⊆ C, maka Cl(A) ⊆ C
Jika \( C \) adalah himpunan tertutup yang memuat \( A \), maka penutupan \( A \), yaitu \( \text{Cl}(A) \), juga harus berada di dalam \( C \). Hal ini mengikuti dari fakta bahwa \( \text{Cl}(A) \) adalah himpunan tertutup terkecil yang memuat \( A \). - Jika A ⊆ B, maka Cl(A) ⊆ Cl(B)
Inklusi himpunan dipertahankan oleh operasi penutupan. Jika \( A \subseteq B \), maka secara otomatis \( \text{Cl}(A) \subseteq \text{Cl}(B) \). - Suatu himpunan A tertutup jika dan hanya jika A = Cl(A)
Sebuah himpunan dikatakan tertutup apabila sama dengan penutupannya. Artinya, himpunan tersebut telah memuat semua titik limitnya. - Penutupan suatu himpunan adalah gabungan himpunan tersebut dengan titik-titik limitnya
Jika \( A' \) menyatakan himpunan titik limit dari \( A \), maka: $$ \text{Cl}(A) = A \cup A' $$ - Idempoten
Operasi penutupan bersifat idempoten, artinya penerapan berulang tidak mengubah hasil: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - Invariansi terhadap himpunan
Setiap himpunan selalu merupakan subhimpunan dari penutupannya: $$ A \subseteq \text{Cl}(A) $$
Akan dilanjutkan.