Himpunan Tertutup
Dalam ruang topologi X, sebuah himpunan B disebut himpunan tertutup jika untuk setiap elemen u yang berada di luar B (yakni dalam komplemennya X-B), selalu ada lingkungan (neighborhood) yang seluruhnya masih berada di dalam komplemen tersebut.
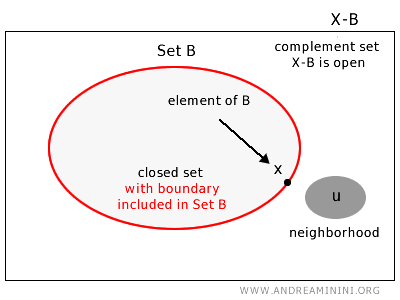
Secara intuitif, sebuah himpunan dikatakan tertutup ketika seluruh titik batasnya termasuk di dalam himpunan itu sendiri.
Secara formal, himpunan B di ruang topologi X adalah himpunan tertutup jika komplemennya, yaitu X-B, merupakan himpunan terbuka.
Catatan: Dalam himpunan tertutup, terdapat titik-titik di mana tidak mungkin membentuk lingkungan kecil yang sepenuhnya berada di dalam himpunan tersebut.
Contoh Dasar
Pertimbangkan garis bilangan real R dan interval tertutup di dalamnya.
Definisi interval tertutup: Interval tertutup [a,b] adalah himpunan semua titik x yang memenuhi a ≤ x ≤ b, dengan a dan b bilangan real, a < b, dan kedua ujung interval termasuk dalam himpunan.
Simbol [a,b] menunjukkan bahwa titik a dan b berada di dalam himpunan tersebut.
Contohnya, interval [3,10] adalah himpunan tertutup pada garis bilangan real.
Dalam hal ini, himpunan B mencakup seluruh bilangan antara 3 dan 10, termasuk kedua titik batasnya.
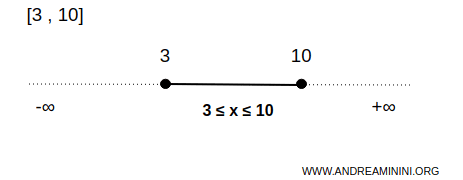
Semua titik x yang memenuhi 3 ≤ x ≤ 10 termasuk dalam himpunan ini. Namun, titik-titik di tepi seperti 3 dan 10 tidak memiliki lingkungan yang sepenuhnya berada di dalam interval tersebut.
Catatan: Misalnya, lingkungan 3 ± 0.00000001 tidak seluruhnya berada di dalam [3,10] karena 3-0.00000001 lebih kecil dari 3. Hal yang sama berlaku untuk titik 10. Tidak ada lingkungan di sekitar 10 yang sepenuhnya berada di dalam [3,10].
Inilah contoh sederhana dari himpunan tertutup satu dimensi.
Himpunan Tertutup di Bidang Datar
Konsep ini juga berlaku di ruang dua dimensi, misalnya pada bidang koordinat.
Pertimbangkan himpunan semua titik yang memenuhi:
$$ x^2 + y^2 ≤ 1 $$
Himpunan ini menggambarkan semua titik yang jaraknya dari pusat (0,0) kurang dari atau sama dengan 1. Dengan kata lain, ia mencakup seluruh titik di dalam lingkaran serta di kelilingnya.
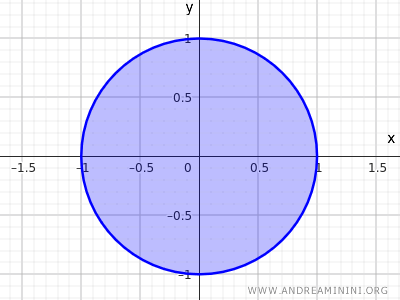
Titik-titik di tepi lingkaran tidak memiliki lingkungan yang sepenuhnya berada di dalam himpunan, tetapi karena tepi tersebut termasuk di dalamnya, himpunan ini tetap disebut tertutup.
Catatan: Dalam topologi Euclidean, lingkaran yang hanya mencakup tepinya ($x^2 + y^2 = 1$) bukan himpunan tertutup, karena tidak mencakup bagian dalamnya. Sebaliknya, himpunan titik yang memenuhi $x^2 + y^2 ≤ 1$ merupakan himpunan tertutup karena mencakup seluruh titik batasnya.
Dengan cara serupa, ide ini bisa diperluas ke ruang tiga dimensi (bola) dan bahkan ke ruang berdimensi lebih tinggi.
Komplemen dari Himpunan Tertutup
Dalam ruang X, komplemen dari himpunan tertutup C adalah himpunan terbuka, dilambangkan dengan X-C.
Artinya, jika C tertutup, maka komplemennya X-C pasti terbuka.
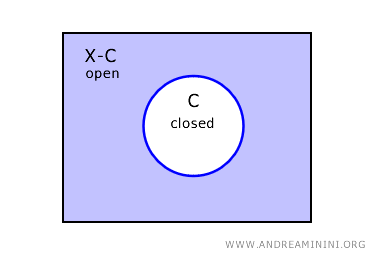
Sebaliknya, jika suatu himpunan U terbuka, maka komplemennya (X-U) adalah himpunan tertutup.
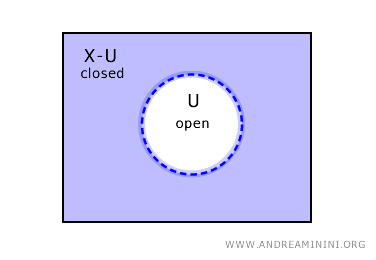
Namun, tidak semua himpunan hanya bisa dikategorikan sebagai terbuka atau tertutup. Dalam topologi, ada juga himpunan yang sekaligus terbuka dan tertutup serta himpunan yang bukan keduanya.
Sederhananya, "tidak tertutup" tidak otomatis berarti "terbuka", dan sebaliknya.
Contoh di Ruang Diskret
Pertimbangkan himpunan X = {a,b,c,d} dengan topologi T tertentu.
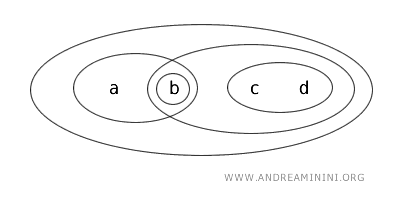
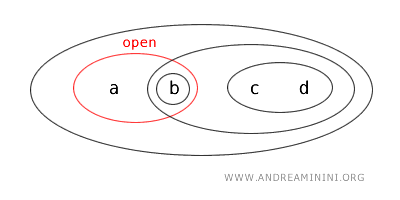
Dalam topologi T, himpunan-himpunan berikut dianggap terbuka: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, dan Ø.
- {b} adalah himpunan terbuka sesuai dengan definisi topologi.
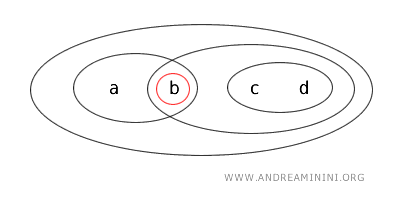
- {a} adalah himpunan tertutup karena merupakan komplemen dari himpunan terbuka {b,c,d}.
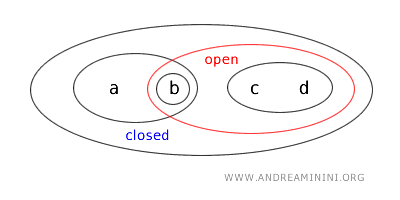
- {a,b} adalah himpunan yang sekaligus terbuka dan tertutup ("clopen"), karena baik himpunan ini maupun komplemennya {c,d} sama-sama terbuka.
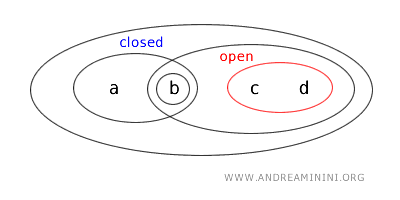
- {b,c} bukan himpunan terbuka maupun tertutup karena tidak memenuhi salah satu kriteria tersebut.
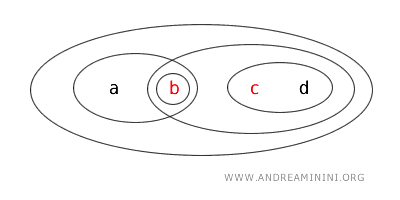
Contoh ini memperlihatkan bahwa dalam topologi, sebuah himpunan bisa terbuka, tertutup, keduanya, atau tidak keduanya.
Sifat-Sifat Utama
Himpunan tertutup memiliki beberapa sifat mendasar:
- Himpunan kosong (Ø) dan seluruh ruang (X) selalu tertutup.
- Irisan dari sembarang himpunan tertutup juga tertutup.
- Gabungan sejumlah terbatas himpunan tertutup tetap tertutup.
Contoh Tambahan
Dalam topologi standar ruang Euclidean Rn, setiap titik tunggal merupakan himpunan tertutup.
Misalnya, untuk satu titik n pada garis bilangan (R1), komplemennya terdiri dari semua titik lain pada R kecuali n.
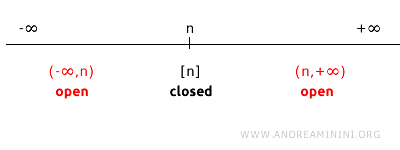
Komplemen {n} adalah gabungan dua interval terbuka: (-∞, n) ∪ (n, +∞). Karena kedua interval ini terbuka, maka gabungannya juga terbuka. Artinya, {n} adalah himpunan tertutup.
Catatan penting: Tidak semua titik tunggal selalu tertutup. Hal ini tergantung pada topologi ruangnya. Misalnya, pada topologi yang dibentuk dari interval terbuka (n, n + 1) untuk setiap bilangan bulat n, titik-titik tunggal tidak tertutup karena tidak mencakup batas di sekitarnya.
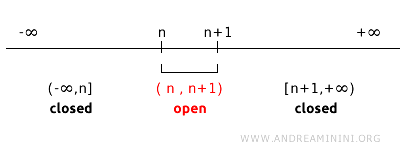
Dalam topologi ini, (1,2) dan (2,3) adalah himpunan terbuka. Komplemennya masing-masing adalah (-∞,1] ∪ [2,+∞) dan (-∞,2] ∪ [3,+∞). Maka, tidak ada komplemen yang membuat {2} menjadi tertutup. Ini menunjukkan bahwa sifat tertutup bergantung pada topologi yang digunakan.
Catatan Penutup
- Hubungan dengan Titik Limit
Titik limit suatu himpunan adalah titik yang di sekelilingnya, sekecil apa pun lingkungan yang diambil, selalu terdapat titik lain dari himpunan tersebut. Himpunan tertutup mencakup seluruh titik limitnya, sementara himpunan terbuka tidak selalu demikian.Contoh: Interval tertutup [0,1] di garis real mencakup semua titik limitnya, termasuk titik batas 0 dan 1, karena di sekitar titik-titik tersebut selalu ada titik lain dalam interval.
![contoh titik limit pada interval [0,1]](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
![titik batas pada interval [0,1]](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-2.gif)
- Himpunan A tertutup jika dan hanya jika A = Cl(A)
Dalam ruang topologi, sebuah himpunan A dikatakan tertutup jika sama dengan penutupannya, yaitu A = Cl(A). Penutupan Cl(A) mencakup semua titik A serta semua titik limitnya. Dengan demikian, himpunan tertutup adalah himpunan yang memuat semua titik limitnya.
Konsep ini menjadi dasar penting dalam analisis matematika dan topologi, karena sifat tertutup menentukan bagaimana himpunan berinteraksi dengan ruang di sekitarnya.