Titik Tetap dalam Topologi
Titik tetap dalam topologi adalah nilai yang tidak berubah meskipun kita menerapkan suatu fungsi padanya. Dengan kata lain, fungsi tersebut "mengembalikan" nilai yang sama seperti yang dimasukkan.
Secara matematis, jika kita memiliki fungsi f(x), maka titik tetap p adalah nilai di mana f(p) = p.
$$ f(p) = p $$
Bayangkan kamu sedang memutar sebuah benda di sekitar titik pusat P. Selama rotasi terjadi, semua titik di benda berpindah posisi - kecuali titik pusatnya.
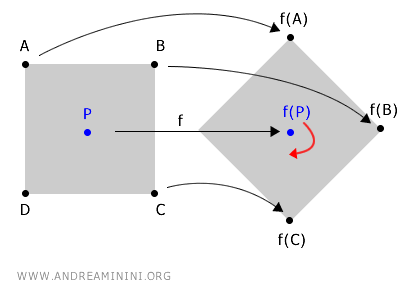
Titik pusat P itulah yang disebut titik tetap, karena posisinya tidak berubah setelah fungsi rotasi f(P) diterapkan.
$$ f(P) \longrightarrow P $$
Konsep sederhana ini ternyata sangat penting, bukan hanya dalam topologi, tetapi juga dalam analisis numerik, teori permainan, bahkan ekonomi - di mana "titik tetap" bisa diartikan sebagai kondisi keseimbangan.
Salah satu hasil paling terkenal yang membahas hal ini adalah Teorema Titik Tetap Brouwer.
Contoh yang Mudah Dipahami
Coba lihat fungsi f(x) = sin(x) pada interval [0, 2π] radian.
$$ f(x) = \sin(x) $$
Titik tetapnya mudah ditemukan di p = 0, karena sin(0) = 0.
$$ \sin(0) = 0 $$
Pada titik ini, nilai keluaran sama persis dengan nilai masukan - inilah yang dimaksud dengan titik tetap.
Contoh 2
Sekarang perhatikan fungsi f(x) = cos(x) pada interval yang sama.
$$ f(x) = \cos(x) $$
Kali ini, x = 0 bukan titik tetap karena cos(0) = 1, jadi nilainya tidak cocok.
Namun, jika kita mencari lebih dalam, akan ditemukan titik tetap pada sekitar x = 0.73908513.
$$ \cos(0.73908513) = 0.73908513 $$
Artinya, pada nilai tersebut fungsi cos(x) dan x saling "bertemu" - sebuah keseimbangan alami antara input dan output.
Teorema Titik Tetap Brouwer
Teorema ini menyatakan sesuatu yang luar biasa:
Setiap fungsi kontinu yang memetakan interval tertutup berdimensi-n ke dirinya sendiri pasti memiliki setidaknya satu titik tetap.
Teorema ini bukan tentang bagaimana menemukan titiknya, melainkan tentang kepastian bahwa titik seperti itu pasti ada.
Ide ini menjadi dasar bagi banyak bidang ilmu - dari matematika murni hingga ekonomi - karena menjelaskan mengapa sistem yang tampak kompleks sering kali cenderung mencapai keseimbangan.
Dan itulah keindahan topologi: dari konsep yang tampak abstrak, kita bisa memahami pola keseimbangan yang berlaku di seluruh alam semesta.