Ruang Regular dalam Topologi

Dalam teori topologi, ruang regular menawarkan tingkat pemisahan yang lebih kuat dibandingkan ruang Hausdorff. Kemampuannya bukan hanya membedakan dua titik, tetapi juga memastikan bahwa titik dan himpunan tertutup yang terpisah dapat dipisahkan dengan lingkungan terbuka yang tidak beririsan.

Jika sebuah ruang regular memiliki basis terhitung, Teorema Urysohn menjamin bahwa ruang tersebut dapat dimetrisasi, sehingga strukturnya dapat dipahami melalui jarak seperti pada ruang metrik.

Perbandingan dengan ruang Hausdorff

Pada ruang Hausdorff, fokusnya adalah pemisahan titik. Pada ruang regular, persyaratannya lebih kuat: pemisahan juga harus berlaku antara titik dan himpunan tertutup. Hal ini membuat regularitas menjadi konsep penting dalam memahami bagaimana ruang topologis mengatur dan memisahkan objek-objek di dalamnya.

Note. Regularitas berbeda dari normalitas. Ruang normal memerlukan syarat tambahan, yaitu dua himpunan tertutup yang saling lepas harus dapat dipisahkan oleh dua lingkungan terbuka yang juga saling lepas. Karena itu, setiap ruang normal pasti regular, namun tidak setiap ruang regular normal.  

Regularitas adalah salah satu dari berbagai aksioma pemisahan. Sebuah ruang dapat regular tanpa menjadi Hausdorff, dan sebaliknya. Terdapat contoh ruang Hausdorff yang tidak regular dan sebaliknya.

Contoh Praktis

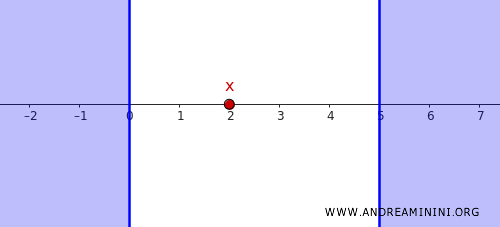
Salah satu contoh paling dikenal dari ruang regular adalah garis bilangan real \( \mathbb{R} \) dengan topologi standar.

Misalkan kita ingin memisahkan sebuah titik \( x = 2 \) dari himpunan tertutup berikut:

\[ C = (-\infty, 0] \cup [5, \infty) \]

Himpunan \( C \) jelas tertutup, dan titik \( 2 \) tidak termasuk di dalamnya.

Komplemen himpunan ini adalah himpunan terbuka yang luas, sehingga kita dapat memilih interval terbuka yang memuat titik \( x \). Misalnya:

\[ (0, 5) \]

Kita kemudian memilih dua bilangan \( c \) dan \( d \) yang mengapit titik \( 2 \):

\[ 0 < c < 2 < d < 5 \]

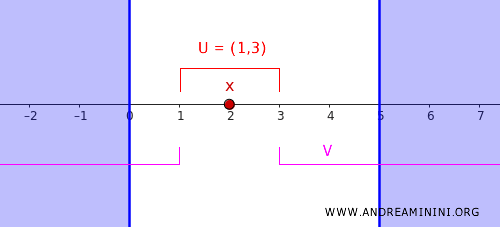
Contoh sederhana adalah \( c = 1 \) dan \( d = 3 \).

Dengan nilai ini, kita dapat mendefinisikan dua himpunan terbuka:

• \( U = (1,3) \), yang merupakan lingkungan terbuka bagi titik \( x = 2 \).
• \( V = (-\infty, 1) \cup (3, \infty) \), yang memuat seluruh himpunan tertutup \( C \).

Kedua himpunan ini tidak beririsan sama sekali, sehingga memenuhi syarat pemisahan pada ruang regular.

Contoh ini menunjukkan dengan jelas bagaimana garis real dengan topologi standar memenuhi definisi ruang regular: titik tunggal dan himpunan tertutup yang terpisah dapat dipisahkan oleh lingkungan terbuka yang berbeda.

Catatan

Untuk memahami peran ruang regular dalam topologi, penting untuk melihatnya sebagai bagian dari sistem yang lebih luas, yaitu aksioma pemisahan. Aksioma-aksioma ini membantu menjelaskan seberapa baik sebuah topologi dapat membedakan titik dan himpunan.

• Aksioma pemisahan
  Regularitas dan sifat Hausdorff adalah dua di antara beberapa tingkat pemisahan yang digunakan untuk mengklasifikasikan ruang topologis. Keduanya menjelaskan bagaimana sebuah ruang memberikan struktur yang cukup halus untuk membedakan objek-objek yang berbeda.

  Note. Sebuah ruang bersifat Hausdorff jika dua titik berbeda dapat dipisahkan oleh lingkungan terbuka yang tidak beririsan. Ruang bersifat regular jika hubungan pemisahan serupa berlaku antara titik dan himpunan tertutup. Tingkat pemisahan ini membantu menggambarkan seberapa halus topologi sebuah ruang.

Regularitas adalah salah satu konsep yang membuka jalan untuk memahami struktur yang lebih kaya dalam topologi, terutama ketika ruang tersebut juga memenuhi sifat-sifat lain seperti normalitas atau metrisabilitas.