Topologi Standar pada Himpunan Terbuka

Topologi standar pada R adalah cara paling umum untuk menentukan mana saja himpunan yang dianggap terbuka. Dalam pendekatan ini, setiap interval terbuka (a, b) dengan a < b, serta setiap gabungan, baik terbatas maupun tak terbatas, dari interval-interval tersebut, didefinisikan sebagai himpunan terbuka.

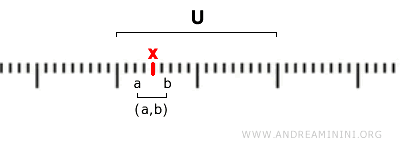
Secara sederhana, suatu himpunan U dikatakan terbuka jika untuk setiap titik x di dalamnya terdapat interval terbuka (a, b) sehingga x termasuk dalam (a, b) dan (a, b) sepenuhnya berada di dalam U.

$$ x \in (a,b) \subseteq U $$

Dengan kata lain, setiap elemen dari himpunan terbuka U selalu memiliki “ruang” di sekitarnya yang juga termasuk dalam U.

Berikut beberapa contoh himpunan terbuka dalam topologi standar:

• Interval Terbuka
  Dalam topologi standar pada \( \mathbb{R} \), himpunan terbuka dapat berupa interval \( (a, b) \) dengan a < b, maupun gabungan dari banyak interval semacam itu, tanpa batasan jumlah.
• Operasi Himpunan
  Himpunan terbuka juga stabil terhadap operasi gabungan dan irisan terbatas.
  • Gabungan: Gabungan dari beberapa himpunan terbuka, berapa pun banyaknya, selalu menghasilkan himpunan terbuka.
  • Irisan Terbatas: Irisan dari sejumlah terbatas himpunan terbuka juga tetap terbuka.

Topologi standar hanyalah salah satu dari berbagai topologi yang bisa didefinisikan pada sebuah himpunan X. Disebut “standar” karena sifatnya yang mendasar dan penggunaannya yang luas di berbagai bidang matematika, terutama dalam analisis dan geometri.

Topologi ini menggambarkan dengan baik gagasan intuitif tentang kedekatan, keterbukaan, dan kekontinuan pada garis bilangan real R, sehingga menjadi pilihan utama dalam banyak konteks.

Catatan: Ada topologi lain pada R maupun pada himpunan lain yang memiliki basis berbeda. Hasilnya, definisi “himpunan terbuka” pun dapat berubah. Biasanya, topologi-topologi alternatif ini digunakan untuk meneliti sifat khusus atau mengkaji struktur matematika dari perspektif yang berbeda.

Contoh Praktis

Basis topologi standar pada garis bilangan real R mencakup semua interval terbuka (a, b) dengan a < b.

$$ B = \{ (a,b) \subset; R \ | \ a \lt b \} $$

Salah satu ciri penting topologi ini adalah bahwa untuk setiap titik x di dalam suatu interval, selalu bisa ditemukan interval terbuka yang lebih kecil di sekitar x, seluruhnya berada di dalam interval semula. Inilah yang membuat suatu himpunan disebut terbuka dalam topologi standar.

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

Topologi ini disebut “standar” karena merupakan cara paling umum dan intuitif untuk memahami keterbukaan pada garis bilangan real.

Contoh 2

Pertimbangkan interval bilangan real (0,1), tanpa menyertakan 0 dan 1, lalu terapkan topologi standar. Apakah interval ini dapat dianggap sebagai sebuah ruang topologi?

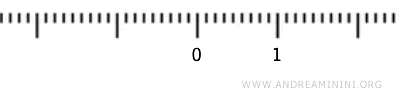
Dalam praktiknya, suatu himpunan bagian \( U \subset (0, 1) \) terbuka jika untuk setiap titik \( x \in U \), ada interval terbuka \( (a, b) \) di \( \mathbb{R} \) sehingga \( x \in (a, b) \) dan \( (a, b) \cap (0, 1) \subseteq U \).

Perhatikan bahwa interval (0,1) sendiri merupakan hasil irisan dari himpunan-himpunan terbuka dalam topologi standar R.

Dengan demikian, interval \( (0, 1) \) membentuk ruang topologi dengan topologi yang diturunkan dari topologi standar \( \mathbb{R} \).

Contohnya, \( (0.1, 0.5) \), \( (0.2, 0.9) \), atau gabungan seperti \( (0.1, 0.5) \cup (0.6, 0.8) \), semuanya merupakan himpunan terbuka dalam \( (0, 1) \) berdasarkan topologi turunan. Dengan kata lain, himpunan terbuka dalam \( (0, 1) \) adalah himpunan terbuka di R yang dibatasi oleh interval \( (0, 1) \).

Karena \( (0, 1) \) merupakan subruang dari \( \mathbb{R} \), topologi yang diturunkan ini tetap mempertahankan semua sifat dasar ruang topologi.

Contoh 3

Sekarang, pertimbangkan himpunan berhingga X = {1, 2, 3} yang terdiri atas tiga bilangan bulat.

Dapatkah himpunan ini dianggap sebagai ruang topologi dalam topologi standar $ \mathbb{R} $? Jawabannya tidak. Dalam topologi standar, interval terbuka digunakan sebagai dasar pembentukan himpunan terbuka, dan konsep ini tidak bisa diterapkan langsung pada himpunan diskret seperti X.

Sebagai ilustrasi, jika elemen {2} dalam X dianggap sebagai bilangan real, elemen ini memang berada dalam interval terbuka (2-ε, 2+ε), tetapi titik-titik lain dalam interval tersebut adalah bilangan real yang tidak termasuk dalam X. Karena itu, syarat keterbukaan dalam topologi standar R tidak terpenuhi.

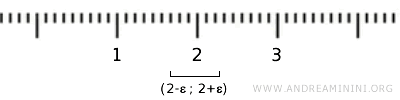
Jika X dianggap sebagai himpunan bagian dari \( \mathbb{R} \), maka dengan menerapkan “topologi turunan” atau “topologi subruang”, himpunan terbuka pada X hanya mencakup himpunan kosong dan X itu sendiri. Hal ini kurang menarik dari sudut pandang topologi.

Untuk membangun ruang topologi dari himpunan berhingga seperti X, topologi diskrit adalah pilihan yang lebih tepat. Dalam topologi diskrit, setiap himpunan bagian dari X secara definisi merupakan himpunan terbuka.

Dengan memahami konsep topologi standar, kita memperoleh dasar penting untuk mempelajari berbagai struktur ruang dalam matematika modern.