Konektivitas dalam Topologi

Dalam topologi, sebuah ruang disebut terhubung jika tidak dapat dipisahkan menjadi dua himpunan terbuka yang saling terpisah. Artinya, konektivitas menggambarkan kemampuan ruang untuk menghubungkan sepasang titik mana pun di dalamnya melalui jalur kontinu tanpa keluar dari batas ruang tersebut.

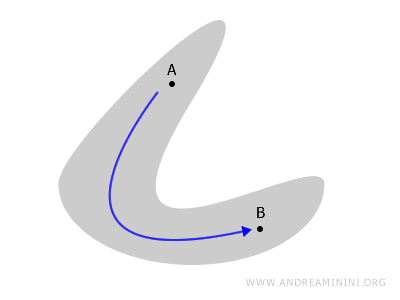
Konektivitas menjelaskan bagaimana bagian-bagian dalam suatu ruang topologi saling berkaitan atau justru terpisah.

Ini merupakan sifat topologis karena didefinisikan dalam istilah himpunan terbuka.

Konsep ini merupakan salah satu pilar utama dalam topologi, sejajar dengan konsep kontinuitas.

Konektivitas sangat penting dalam berbagai cabang matematika karena memberikan pemahaman mendalam mengenai struktur ruang serta hubungan antar komponennya. Misalnya, konsep ini mempermudah klasifikasi maupun analisis ruang topologi.

Contoh Praktis

Sebuah ruang, baik berupa bidang datar maupun bangun ruang, dikatakan terhubung apabila selalu ada jalur kontinu yang dapat menghubungkan titik A dan B di dalamnya tanpa keluar dari ruang tersebut.

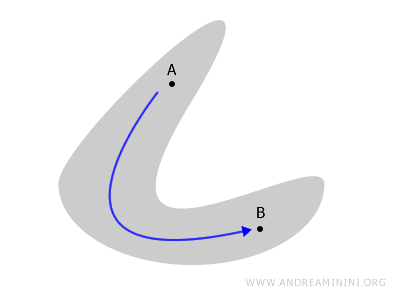
Sebaliknya, jika sebagian ruang terpisah sehingga tidak ada jalur kontinu di antara keduanya, maka ruang tersebut tidak terhubung.

Contohnya, bila ruang terbagi menjadi dua bagian yang saling lepas, setiap jalur yang ingin menghubungkan titik A dan B harus melewati luar ruang tersebut.

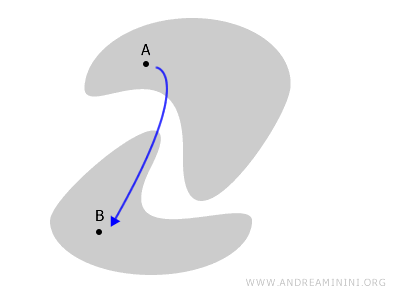
Penting untuk meninjau lebih jauh konsep ruang tak terhubung melalui ilustrasi yang lebih konkret.

Kapan sebuah ruang dianggap tak terhubung?

Bayangkan dua ruangan dalam satu bangunan yang dipisahkan oleh dinding. Kedua ruangan ini dapat dilihat sebagai dua himpunan terbuka yang tidak mencakup batasnya (dinding) dan terpisah satu sama lain.

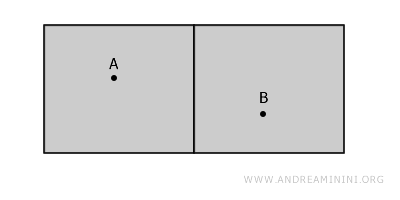
Meski sekilas tampak seolah-olah ruangan itu menyatu, sebenarnya tidak, sebab jalur dari titik A ke titik B pasti harus melewati dinding, yang berada di luar ruang yang didefinisikan.

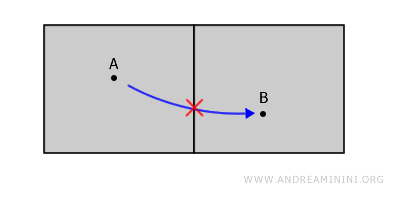
Dengan kata lain, batas ruang tidak termasuk dalam himpunan terbuka.

Konektivitas Lokal

Konektivitas lokal muncul ketika setiap himpunan terbuka dalam ruang, meski terpisah dari himpunan lain, tetap memiliki lingkungan (neighborhood) yang terhubung. Dengan kata lain, setiap titik memiliki himpunan terbuka terhubung yang melingkupinya.

Misalnya, sebuah ruang yang terdiri dari dua himpunan terbuka terpisah, seperti dua ruangan berbeda dalam satu bangunan.

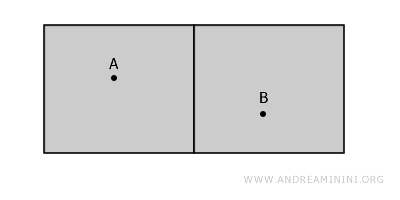
Ruang ini jelas tidak terhubung karena tidak ada jalur yang bisa menghubungkan titik A dan B tanpa melewati dinding.

Namun, di sekitar titik A terdapat himpunan terbuka yang seluruh unsurnya saling terhubung, sehingga menunjukkan adanya konektivitas lokal.

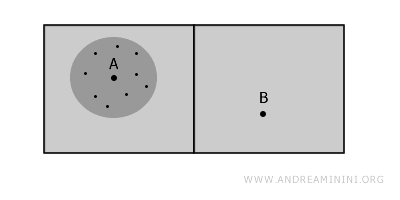
Hal yang sama berlaku untuk titik B, yang juga memiliki konektivitas lokal.

Jenis-jenis Konektivitas

Ada berbagai macam bentuk konektivitas. Dua yang paling umum adalah:

• Keterhubungan Topologis
  Sebuah ruang topologi $ X $ dikatakan terhubung apabila ruang tersebut tidak dapat dipisahkan menjadi dua himpunan terbuka yang saling lepas dan tidak kosong, yang bila digabungkan membentuk seluruh ruang. Dengan kata lain, tidak ada cara untuk “memecah” ruang tersebut menjadi dua bagian terbuka yang sepenuhnya terpisah.

  Contoh. Ruang $(-1, 1)$ merupakan ruang yang terhubung, sedangkan ruang $(-1, 0) \cup (0, 1)$ tidak terhubung. Hal ini karena terdapat dua himpunan terbuka yang tidak kosong dan saling lepas, yaitu $(-1, 0)$ dan $(0, 1)$, yang bila digabungkan mencakup seluruh ruang.
  Kedua himpunan ini dengan demikian membentuk suatu pemisahan dari ruang tersebut.

• Keterhubungan Lintasan (atau Keterhubungan Busur)
  Sebuah ruang topologi disebut terhubung lintasan jika untuk setiap dua titik A dan B di dalam ruang tersebut terdapat lintasan kontinu yang menghubungkan keduanya dan seluruhnya berada di dalam ruang itu sendiri. Setiap ruang yang terhubung lintasan pasti terhubung, meskipun tidak semua ruang terhubung memiliki sifat keterhubungan lintasan.

  Contoh. Bayangkan sebuah bentuk tertutup di bidang datar. Untuk setiap dua titik di dalamnya, kita dapat menggambar sebuah kurva kontinu yang menghubungkan keduanya tanpa mengangkat pena dari kertas dan tanpa keluar dari bentuk tersebut.
  
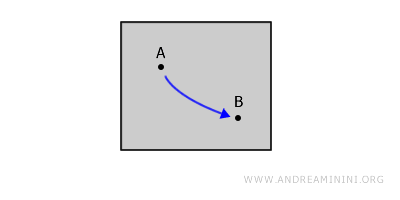
  Perbedaan antara keterhubungan busur dan keterhubungan lintasan. Keduanya serupa, namun pada keterhubungan busur, lintasan harus bersifat satu-ke-satu - artinya tidak boleh berpotongan atau melewati titik yang sama lebih dari sekali.

• Konektivitas Sederhana
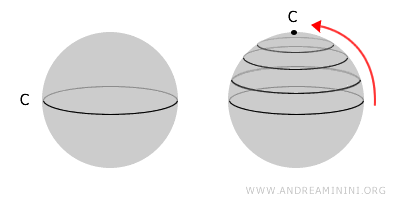
  Sebuah ruang disebut terhubung sederhana jika setiap lintasan tertutup di dalamnya dapat diciutkan menjadi sebuah titik. Ini berarti ruang tersebut menyatu tanpa lubang internal. Ruang terhubung sederhana selalu terhubung, tetapi tidak semua ruang terhubung bersifat sederhana. Secara formal, dalam ruang topologi yang terhubung sederhana, setiap lintasan homotopik terhadap sebuah titik.

  Misalnya, sebuah bola merupakan ruang terhubung sederhana karena setiap lintasan di permukaannya bisa diciutkan menjadi titik. Sebaliknya, torus (donat) dengan lubang di tengah tidak memungkinkan semua lintasan diciutkan menjadi titik. Maka, torus adalah ruang yang terhubung namun tidak sederhana.
  
  
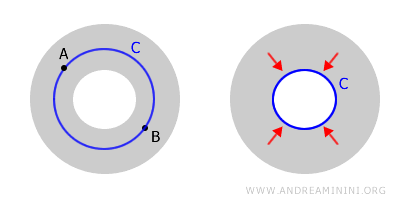
  Ruang semacam ini, terhubung namun tidak sederhana, disebut ruang multi-terhubung. Contoh klasiknya adalah ruang berbentuk cincin.

Catatan

Beberapa hal penting untuk dicatat:

• Dalam bilangan real, satu-satunya ruang yang terhubung adalah interval.