Batas Suatu Himpunan

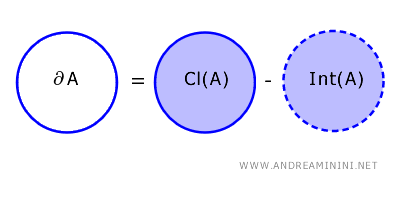
Batas dari suatu subhimpunan $ A $ dalam ruang topologi $ X $ adalah himpunan titik-titik yang berada dalam penutupan $ A $, tetapi tidak termasuk dalam interiornya. Secara formal, batas didefinisikan sebagai: \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

Di sini, $ \text{Cl}(A) $ adalah penutupan dari $ A $, yaitu himpunan yang memuat semua titik $ A $ beserta seluruh titik limitnya.

Sementara itu, $ \text{Int}(A) $ adalah interior dari $ A $, yakni kumpulan semua titik dalam $ A $ yang memiliki suatu lingkungan terbuka yang sepenuhnya berada di dalam $ A $.

contoh batas suatu himpunan

Perlu dicatat bahwa batas bukanlah sifat bawaan dari suatu himpunan. Nilainya sangat bergantung pada topologi yang digunakan pada ruang tersebut.

Akibatnya, sebuah himpunan dapat memiliki batas yang berbeda jika ditinjau dengan topologi yang berbeda pula.

Secara intuitif, batas himpunan $ A $ terdiri dari titik-titik yang berada sangat dekat dengan $ A $, sekaligus sangat dekat dengan komplemennya $ X \setminus A $.

Contoh Praktis
Teorema Batas
Catatan

Contoh Praktis

Misalkan $ A = (0, 1) $ adalah subhimpunan dari garis bilangan real $ \mathbb{R} $ dengan topologi standar.

Kita akan menentukan batas dari himpunan $ A $ langkah demi langkah.

1] Menentukan Penutupan A

Penutupan dari $ A $, yang dilambangkan dengan $ \text{Cl}(A) $, mencakup semua titik dalam $ A $ serta titik-titik limitnya.

Untuk $ A = (0, 1) $, penutupannya adalah interval tertutup $[0, 1]$. Hal ini terjadi karena setiap titik di dalam $(0, 1)$ merupakan titik limit, dan titik 0 serta 1 merupakan titik ujung interval.

$$ \text{Cl}(A) = [0, 1] $$

2] Menentukan Interior A

Interior dari $ A $, yang dilambangkan dengan $ \text{Int}(A) $, adalah himpunan semua titik dalam $ A $ yang memiliki lingkungan terbuka yang sepenuhnya terkandung di dalam $ A $.

Untuk interval terbuka $ (0, 1) $, interiornya adalah himpunan itu sendiri, karena setiap titik di dalamnya memiliki lingkungan yang tetap berada di dalam interval.

$$ \text{Int}(A) = (0, 1) $$

3] Menentukan Batas A

Batas dari $ A $ diperoleh dengan mengambil selisih antara penutupan dan interior:

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

Dengan memasukkan hasil sebelumnya, diperoleh:

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

Dengan demikian, pada topologi standar di $ \mathbb{R} $, batas dari himpunan $ A = (0,1) $ adalah himpunan titik $\{0, 1\}$.

Kedua titik ini berada tepat di peralihan antara bagian dalam dan bagian luar $ A $, sehingga secara alami merepresentasikan batas himpunan tersebut.

contoh batas himpunan

Teorema Batas

Suatu titik $ x $ dalam ruang topologi $ X $ termasuk dalam batas $ \partial A $ dari suatu subhimpunan $ A $ jika dan hanya jika setiap lingkungan dari $ x $ beririsan dengan $ A $ dan juga dengan komplemennya, yaitu $ X - A $.

Teorema ini memberikan cara praktis untuk memeriksa apakah sebuah titik termasuk dalam batas suatu himpunan.

Contoh

Kembali kita tinjau himpunan $ A = (0, 1) $ pada garis bilangan real $ \mathbb{R} $ dengan topologi standar.

Penutupan dan interiornya adalah:

$$ \text{Cl}(A) = [0, 1] $$

$$ \text{Int}(A) = (0, 1) $$

Maka batasnya adalah:

$$ \partial A = \{0, 1\} $$

Berikut ini kita verifikasi secara langsung menggunakan teorema batas.

1] Memeriksa Titik 0

Ambil suatu lingkungan dari 0, misalnya $ (0-\epsilon, 0+\epsilon) $ dengan $ \epsilon > 0 $.

Lingkungan ini selalu beririsan dengan $ A $, karena mengandung titik-titik dalam interval $ (0, 1) $.

Lingkungan tersebut juga beririsan dengan $ X - A $, karena memuat titik-titik yang lebih kecil dari 0.

Oleh sebab itu, $ 0 \in \partial A $.

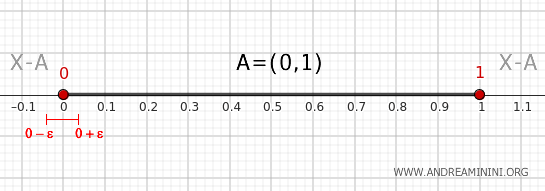
lingkungan titik 0

2] Memeriksa Titik 1

Ambil lingkungan dari 1, misalnya $ (1-\epsilon, 1+\epsilon) $ dengan $ \epsilon > 0 $.

Lingkungan ini beririsan dengan $ A $ dan juga beririsan dengan $ X - A $.

Maka dapat disimpulkan bahwa $ 1 \in \partial A $.

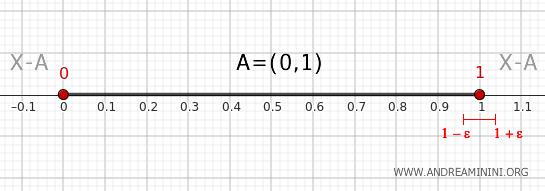
lingkungan titik 1

3] Memeriksa Titik di Dalam (0,1)

Ambil sebuah titik di dalam interval, misalnya 0.5, dan perhatikan lingkungan $ (0.5-\epsilon, 0.5+\epsilon) $.

Lingkungan ini sepenuhnya berada di dalam $ A $ dan tidak beririsan dengan $ X - A $.

Karena itu, $ 0.5 \notin \partial A $.

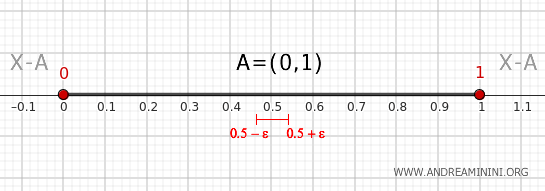
lingkungan titik 0.5

Kesimpulannya, hanya titik 0 dan 1 yang termasuk dalam batas himpunan $ A = (0, 1) $.

Catatan

Beberapa sifat penting dari batas suatu himpunan antara lain:

Batas $ \partial A $ merupakan subhimpunan dari $ A $ jika dan hanya jika $ A $ tertutup
\[ \partial A \subseteq A \Leftrightarrow A \text{ tertutup} \]
Irisan antara batas dan himpunan $ A $ kosong jika dan hanya jika $ A $ terbuka
\[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ terbuka} \]
Batas $ \partial A $ kosong jika dan hanya jika $ A $ bersifat terbuka sekaligus tertutup (clopen)
\[ \partial A = \emptyset \Leftrightarrow A \text{ clopen} \]
Batas $ \partial A $ sama dengan irisan penutupan $ A $ dan penutupan komplemennya
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \]
Batas $ \partial A $ selalu merupakan himpunan tertutup
Irisan dua himpunan tertutup selalu merupakan himpunan tertutup. Karena batas didefinisikan sebagai $\partial A = \text{Cl}(A) \cap \text{Cl}(X - A)$, maka $\partial A$ selalu tertutup.
Irisan antara batas dan interior selalu kosong
\[ \partial A \cap \text{Int}(A) = \emptyset \]
Gabungan antara batas dan interior sama dengan penutupan himpunan
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]

Dan seterusnya.