Memahami Homeomorfisme dalam Topologi

Homeomorfisme adalah konsep penting dalam topologi yang menggambarkan bagaimana satu ruang dapat diubah menjadi ruang lain tanpa merusak strukturnya. Sebuah fungsi disebut homeomorfisme jika bersifat bijektif (satu-satu), kontinu, dan memiliki invers yang juga kontinu.

Artinya, kita bisa mengubah bentuk suatu objek menjadi bentuk lain - lalu kembali lagi - tanpa ada proses “memotong” atau “menempelkan” bagian baru.

Secara intuitif, homeomorfisme memungkinkan bentuk berubah secara mulus tanpa kehilangan sifat dasarnya. Ruang-ruang yang terhubung oleh homeomorfisme disebut ruang homeomorfik, karena secara topologis mereka identik meskipun bentuk geometrinya berbeda.

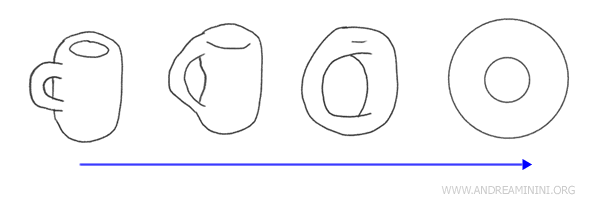
Contohnya cukup terkenal: cangkir kopi dan donat dianggap homeomorfik. Mengapa? Karena keduanya bisa diubah satu sama lain lewat deformasi kontinu - tanpa merobek atau menempelkan apa pun.

Dalam pandangan topologi, keduanya memiliki satu “lubang”: lubang tengah pada donat dan celah pada pegangan cangkir. Jika bagian pegangan cangkir “diregangkan” dan dibentuk ulang, hasilnya akan menjadi donat.

Sifat Utama Homeomorfisme

Berikut empat ciri penting yang membuat suatu fungsi menjadi homeomorfisme:

• Bijektif - Setiap titik di ruang pertama memiliki pasangan unik di ruang kedua, dan sebaliknya.
• Kontinu - Perubahan kecil pada input menghasilkan perubahan kecil pada output, tanpa “lompatan” nilai.
• Invers kontinu - Fungsi kebalikannya juga harus kontinu agar perubahan bisa dibalik dengan mulus.
• Menjaga sifat topologis - Hubungan dasar antar titik (seperti keterhubungan dan kekompakan) tetap sama meskipun bentuknya berubah.

Jadi, homeomorfisme pada dasarnya adalah cara untuk “membentuk ulang” ruang tanpa merusak strukturnya. Ia seperti cermin topologis: dua bentuk yang tampak berbeda tapi sebenarnya setara dari sudut pandang ruang dan hubungan antar titiknya.

Apa Itu Fungsi Kontinu dalam Topologi?

Diberikan dua ruang topologi \(X\) dan \(Y\), suatu fungsi \(f: X \to Y\) dikatakan kontinu jika untuk setiap himpunan terbuka \(V\) di \(Y\), prabentuknya \(f^{-1}(V)\) juga merupakan himpunan terbuka di \(X\).

Dengan kata lain, fungsi kontinu menjaga struktur himpunan terbuka ketika memetakan titik-titik dari satu ruang ke ruang lain.

Berbeda dari analisis matematika yang mengandalkan jarak, topologi tidak memerlukan ukuran jarak sama sekali - cukup dengan memahami bagaimana himpunan terbuka saling berhubungan.

Catatan: Dalam analisis, kontinuitas bergantung pada jarak antara titik-titik. Dalam topologi, ia bergantung pada struktur himpunan terbuka - konsep yang lebih abstrak dan fleksibel.

Contoh Sederhana: Memeriksa Kontinuitas

Bayangkan dua ruang topologi:

\(X = \{a, b, c, d\}\) dan \(Y = \{1, 2\}\).

• Dalam \(X\), himpunan terbukanya adalah: \(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\).
• Dalam \(Y\), himpunan terbukanya adalah: \(\{\}, \{1\}, \{1, 2\}\).

Definisikan fungsi \(f: X \to Y\) berikut:

\(f(a) = 1\), \(f(b) = 1\), \(f(c) = 2\), \(f(d) = 2\).

Untuk memvisualisasikan hubungan ini, bayangkan setiap himpunan terbuka dilingkari agar mudah terlihat keterhubungannya.

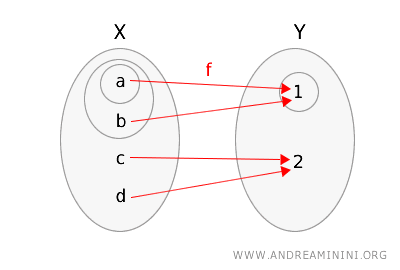
Mari kita uji apakah fungsi tersebut memenuhi syarat kontinuitas:

• Untuk himpunan terbuka \(\{1\}\) di \(Y\), prabentuknya di \(X\) adalah \(f^{-1}(\{1\}) = \{a, b\}\). Himpunan ini terbuka di \(X\).
• Untuk himpunan \(\{1, 2\}\) di \(Y\), prabentuknya adalah \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\), juga terbuka di \(X\).

Karena semua prabentuk himpunan terbuka di \(Y\) juga terbuka di \(X\), maka fungsi \(f\) bersifat kontinu.

Catatan: Himpunan kosong selalu dianggap terbuka dalam ruang topologi mana pun, jadi tidak perlu diperiksa.

Sekarang, kita ubah sedikit fungsinya menjadi \(g: X \to Y\) dengan aturan:

\(g(a) = 1\), \(g(b) = 1\), \(g(c) = 1\), \(g(d) = 2\).

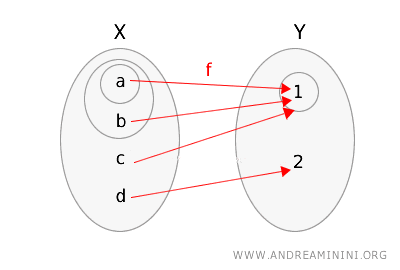
Untuk himpunan terbuka \(\{1\}\) di \(Y\), prabentuknya adalah \(g^{-1}(\{1\}) = \{a, b, c\}\). Himpunan ini tidak terbuka di \(X\), jadi fungsi \(g\) tidak kontinu.

Kesimpulan: Fungsi dikatakan kontinu jika setiap himpunan terbuka di ruang tujuan memiliki prabentuk yang juga terbuka di ruang asal. Dalam contoh kita, fungsi \(f\) memenuhi syarat itu - sedangkan fungsi \(g\) tidak.

Apa Itu Homeomorfisme?

Homeomorfisme adalah konsep dasar dalam topologi yang menjelaskan kapan dua ruang dianggap “sama” dari sudut pandang struktur, meskipun bentuk luarnya berbeda. Secara formal, jika ada fungsi bijektif \( f: X \to Y \) dengan invers \( f^{-1}: Y \to X \), dan keduanya bersifat kontinu, maka \( f \) disebut homeomorfisme. Dalam hal ini, ruang \( X \) dan \( Y \) disebut homeomorfik, ditulis \( X \cong Y \).

Artinya, dua ruang tersebut memiliki susunan topologi yang identik. Mereka boleh berbeda secara geometris, tapi “secara topologis” keduanya setara.

Bayangkan Anda memiliki lembaran kertas yang digulung menjadi silinder. Selama tidak ada bagian yang direkatkan atau disobek, bentuk baru itu tetap memiliki struktur yang sama dengan bentuk semula. Inilah yang disebut homeomorfisme.

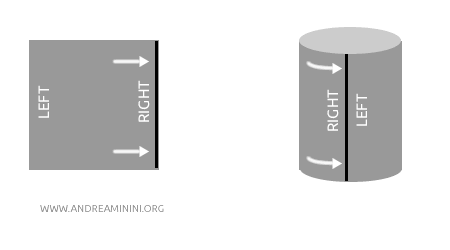
Dengan kata lain, homeomorfisme adalah “cara lembut” untuk mengubah satu bentuk menjadi bentuk lain tanpa merusak koneksi antara titik-titik di dalamnya. Karena itu, dua ruang yang homeomorfik sering disebut setara secara topologis.

Tiga Syarat Penting Homeomorfisme

1. Bijektif - Setiap titik di \( X \) berpasangan tepat dengan satu titik di \( Y \), dan sebaliknya.
2. Kontinu - Perubahan kecil pada \( X \) menghasilkan perubahan kecil pula di \( Y \); tidak ada “lompatan” mendadak.
3. Invers kontinu - Fungsi kebalikannya \( f^{-1} \) juga harus kontinu agar transformasi bisa dibalik dengan mulus.

Contoh visual: Bayangkan kertas yang digulung menjadi silinder lalu dibuka lagi - proses ini bisa dilakukan tanpa merobek atau menempelkan bagian mana pun. Struktur topologinya tetap sama walaupun bentuk geometrinya berubah.

Fungsi Kontinu dan Inversnya

Perlu diingat bahwa tidak semua fungsi bijektif yang kontinu otomatis memiliki invers yang kontinu. Agar fungsi bijektif \( f \) menjadi homeomorfisme, ia juga harus merupakan peta terbuka - yaitu fungsi yang mengubah himpunan terbuka di \( X \) menjadi himpunan terbuka di \( Y \).

Jika syarat ini tidak terpenuhi, maka fungsi tersebut tidak bisa disebut homeomorfisme, walaupun tampak memenuhi sebagian kriterianya.

Contoh 1: Fungsi Bijektif tapi Bukan Homeomorfisme

Pertimbangkan dua ruang topologi:

• \( X = (a, b) \) dengan topologi \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \).
• \( Y = (1, 2) \) dengan topologi \( T_Y = \{\emptyset, Y\} \).

Definisikan fungsi \( f(a) = 1 \) dan \( f(b) = 2 \). Fungsi ini memang bijektif dan kontinu, tapi inversnya tidak kontinu karena topologi \( Y \) terlalu “kasar” - ia hanya punya dua himpunan terbuka: \( \emptyset \) dan \( Y \). Akibatnya, beberapa himpunan di \( X \) tidak punya padanan terbuka di \( Y \).

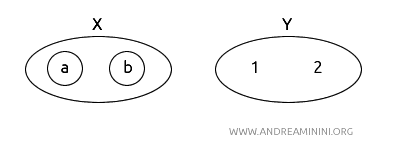
Jadi, \( f \) bukan homeomorfisme.

Contoh 2: Ketika Inversnya Juga Kontinu

Sekarang ubah sedikit topologinya:

• \( X = (a, b) \) dengan \( T_X = \{\emptyset, \{a\}, X\} \).
• \( Y = (1, 2) \) dengan \( T_Y = \{\emptyset, \{1\}, Y\} \).

Dengan definisi fungsi \( f(a) = 1 \) dan \( f(b) = 2 \), kali ini baik \( f \) maupun inversnya \( f^{-1} \) sama-sama kontinu. Maka, \( f \) adalah homeomorfisme.

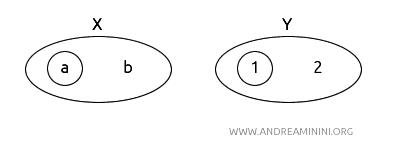
Perbedaan hasilnya bukan pada fungsi, tapi pada topologi yang digunakan. Ini menunjukkan bahwa sifat homeomorfik tergantung sepenuhnya pada struktur topologinya, bukan pada bentuk fisiknya.

Homeomorfisme dan Transformasi Topologis Lain

Homeomorfisme termasuk dalam keluarga besar transformasi topologis - cara-cara untuk mengubah suatu ruang tanpa merusak sifat dasarnya.

• Transformasi topologis mencakup berbagai jenis perubahan yang mempertahankan sifat-sifat utama seperti keterhubungan dan kontinuitas. Contohnya meliputi isotopi, homotopi, dan difeomorfisme.
• Homeomorfisme adalah bentuk khusus dari transformasi topologis yang bersifat bijektif dan kontinu dengan invers yang juga kontinu. Ruang-ruang yang saling homeomorfik bisa dikatakan “berstruktur sama”, meskipun wujudnya berbeda.

Dengan kata lain: semua homeomorfisme adalah transformasi topologis, tetapi tidak semua transformasi topologis adalah homeomorfisme.

Catatan Menarik

• Sifat topologis adalah ciri khas ruang topologi yang tetap tidak berubah di bawah homeomorfisme. Dua ruang yang homeomorfik pasti memiliki sifat topologis yang sama.
• Teorema Hausdorff menyatakan bahwa jika \( X \) adalah ruang Hausdorff dan \( f: X \to Y \) merupakan homeomorfisme, maka \( Y \) juga Hausdorff - karena sifat topologis selalu terpelihara.
• Dalam aljabar, konsep yang sepadan dengan homeomorfisme adalah isomorfisme grup - keduanya menjaga struktur dasar, meskipun dalam konteks yang berbeda.

Singkatnya, homeomorfisme adalah “jembatan lembut” yang menghubungkan dua ruang topologi - menjaga struktur, meskipun bentuknya berubah.