Ruang Hausdorff

Ruang Hausdorff adalah ruang topologi di mana setiap dua titik yang berbeda selalu dapat dipisahkan oleh dua lingkungan terbuka yang tidak saling beririsan. Ini adalah salah satu konsep dasar dalam topologi umum dan menjadi fondasi penting untuk memahami bagaimana "keterpisahan" bekerja dalam ruang abstrak.

Intinya, jika Anda memiliki dua titik $ x $ dan $ y $, pasti ada dua lingkungan terbuka $ U $ dan $ V $ yang tidak bertemu sama sekali sehingga $ U \cap V = \emptyset $. Kondisi pemisahan inilah yang membedakan ruang Hausdorff dari jenis ruang topologi lainnya.

Sifat ini juga mendukung intuisi kita tentang jarak dan kedekatan dalam geometri Euclidean, sehingga ruang Hausdorff sangat berguna dalam analisis dan geometri, terutama ketika membahas perilaku limit barisan dan fungsi.

Konsekuensi penting lain adalah bahwa singleton, yaitu himpunan yang hanya berisi satu titik, selalu merupakan himpunan tertutup. Ini terjadi karena komplemennya - himpunan semua titik lain - selalu terbuka.

Contoh Praktis
Catatan

Contoh Praktis

Contoh 1

Pertimbangkan topologi standar pada garis bilangan real $\mathbb{R}$. Contoh ini sangat umum digunakan dalam buku teks dan kursus dasar topologi.

contoh garis bilangan real

Dalam topologi standar, himpunan satu titik bukan himpunan terbuka.

Penjelasan: Sebuah himpunan terbuka harus memuat interval terbuka penuh di sekitar setiap titik. Karena antara dua bilangan real selalu ada tak terhingga banyak bilangan lain, himpunan tunggal $ \{x\} $ tidak bisa memuat interval terbuka apa pun. Karena itu, ia tidak memenuhi definisi himpunan terbuka.

Namun komplemennya, yaitu $ \mathbb{R} \setminus \{x\} $, selalu terbuka.

lingkungan himpunan satu titik adalah himpunan terbuka

Maka, $ \{x\} $ adalah himpunan tertutup.

Topologi standar juga merupakan ruang Hausdorff karena dua titik berbeda dapat selalu dipisahkan oleh dua interval terbuka yang tidak beririsan.

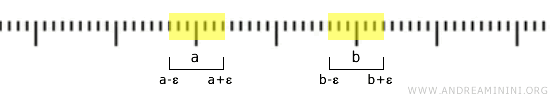
lingkungan titik a dan b

Sebagai contoh, jika $ a < b $, kita dapat memilih interval $ (a-\epsilon, a+\epsilon) $ dan $ (b-\epsilon, b+\epsilon) $ dengan $ \epsilon $ cukup kecil sehingga $ a+\epsilon < b-\epsilon $. Dengan begitu, kedua interval tersebut saling lepas dan syarat pemisahan Hausdorff terpenuhi.

Sifat bahwa singleton selalu tertutup selaras dengan karakter ruang Hausdorff.

Contoh 2

Sekarang lihat contoh yang jauh lebih sederhana: himpunan X = {1,2,3} dengan topologi diskret.

Dalam topologi diskret, setiap himpunan bagian dari X adalah himpunan terbuka. Tidak ada batasan tambahan.

Himpunan kosong $ \emptyset $
Himpunan satu titik $ \{1\} $, $ \{2\} $, $ \{3\} $
Himpunan dua titik $ \{1, 2\} $, $ \{1, 3\} $, $ \{2, 3\} $
Himpunan penuh $ \{1, 2, 3\} $

Totalnya ada $ 2^3 = 8 $ himpunan terbuka. Semua kombinasi mungkin.

Karena setiap himpunan bagian terbuka, memisahkan dua titik berbeda menjadi sangat mudah: cukup pilih $ U = \{x\} $ dan $ V = \{y\} $. Jelas keduanya tidak beririsan, sehingga syarat Hausdorff langsung terpenuhi.

Untuk x={1} dan y={2}, kita mendapat:

$$ \{ 1 \} \cap \{ 2 \} = \emptyset $$

Ini menunjukkan dengan sangat langsung bahwa kedua titik memiliki lingkungan yang terpisah.

Apakah singleton dalam topologi diskret terbuka atau tertutup? Dalam topologi diskret, jawabannya adalah: keduanya. Ini disebut himpunan clopen. Dalam topologi, terbuka dan tertutup bukan dua sifat yang saling meniadakan.

Setiap singleton {x} adalah terbuka karena semua himpunan bagian terbuka. Tetapi {x} juga tertutup karena komplemennya, yaitu X \ {x}, juga himpunan terbuka.

Sebagai contoh, pada X={1,2,3}, himpunan {1} terbuka. Namun komplemennya {2,3} juga terbuka, sehingga {1} otomatis tertutup.

Jadi, dalam topologi diskret, setiap singleton {x} adalah terbuka sekaligus tertutup.

Terbuka: semua himpunan bagian dalam topologi diskret terbuka.
Tertutup: komplemen singleton juga terbuka sehingga singleton merupakan himpunan tertutup.

Perbedaan utama antara topologi diskret dan topologi standar adalah bahwa dalam topologi standar hanya himpunan-himpunan yang memenuhi definisi lingkungan terbuka untuk setiap titik di dalamnya yang dianggap terbuka. Tidak semua himpunan bagian otomatis terbuka seperti pada topologi diskret.

Catatan

Berikut beberapa poin penting yang membantu memahami ruang Hausdorff secara lebih mendalam.

Limit barisan dalam ruang Hausdorff selalu unik
Ini adalah salah satu alasan mengapa ruang Hausdorff sering dianggap sebagai "standar minimal" dalam banyak cabang analisis. Jika sebuah barisan konvergen ke dua limit berbeda, maka lingkungan kedua titik tersebut pasti beririsan, yang bertentangan dengan sifat Hausdorff.
Pembuktian ringkas. Misalkan X adalah ruang Hausdorff, misalnya X=R. Jika barisan x_n konvergen ke dua titik berbeda x dan y, maka mulai indeks tertentu barisan tersebut akan berada dalam lingkungan A dari x, dan mulai indeks lain dalam lingkungan B dari y. Kedua lingkungan tersebut harus beririsan, yang berarti tidak saling lepas. Ini bertentangan dengan definisi ruang Hausdorff. Karena itu, limit barisan harus unik.

Dan seterusnya.