Himpunan Clopen
Dalam topologi, sebuah himpunan disebut "clopen" apabila ia bersifat terbuka sekaligus tertutup pada saat yang sama.
Artinya, himpunan tersebut memenuhi dua kondisi sekaligus dalam topologi yang sama: tidak hanya terbuka, tetapi juga tertutup.
Istilah “clopen” sendiri berasal dari penggabungan dua kata bahasa Inggris, “closed” dan “open.”
Himpunan seperti ini memiliki karakteristik yang biasanya dimiliki oleh himpunan terbuka dan himpunan tertutup secara bersamaan.
Kondisi ini terjadi ketika suatu himpunan dan komplemennya sama-sama terbuka dalam topologi tertentu.
Catatan: Himpunan clopen jarang ditemukan pada himpunan bilangan real, tetapi sering muncul pada ruang topologi yang lebih abstrak. Himpunan ini menarik karena memberikan wawasan unik tentang struktur internal suatu ruang topologi.
Contoh Sederhana
Pertimbangkan himpunan X = {a, b, c, d} dengan topologi T.
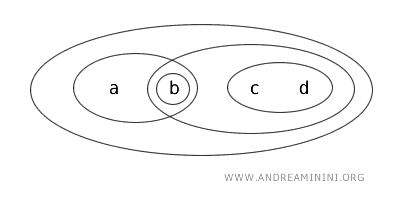
Dalam topologi T, himpunan-himpunan berikut merupakan himpunan terbuka: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, dan Ø.
Maka, himpunan {a,b} termasuk dalam kategori himpunan terbuka di bawah topologi T.
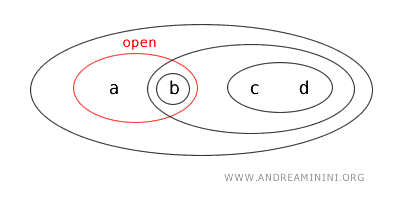
Namun, perhatikan bahwa {a,b} juga merupakan komplemen dari himpunan terbuka {c,d}:
$$ X - \{ c,d \} = \{ a , b \} $$
Karena komplemen dari himpunan terbuka selalu tertutup, maka {a,b} juga merupakan himpunan tertutup.
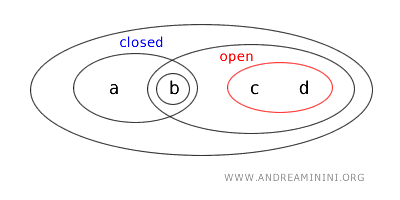
Dengan demikian, dalam topologi T, himpunan {a,b} bersifat terbuka dan tertutup sekaligus. Inilah yang disebut sebagai himpunan clopen.
Himpunan Kosong dan Himpunan Seluruhnya
Dalam setiap topologi pada himpunan X, baik himpunan kosong (∅) maupun himpunan seluruhnya (X) selalu merupakan himpunan clopen, yaitu terbuka dan tertutup sekaligus.
Secara sederhana, sebuah himpunan disebut “clopen” apabila memenuhi dua syarat sekaligus: terbuka dan tertutup dalam topologi yang sama.
Untuk memahami alasannya, mari kita lihat kembali definisi dasarnya.
Menurut definisi topologis himpunan terbuka, himpunan kosong (∅) dan himpunan seluruhnya (X) selalu dianggap terbuka.
Sementara menurut definisi himpunan tertutup, sebuah himpunan dikatakan tertutup apabila komplemennya merupakan himpunan terbuka.
Dari sini dapat disimpulkan bahwa:
- Himpunan kosong (∅)
Himpunan kosong selalu terbuka menurut prinsip dasar topologi. Ia juga tertutup karena komplemennya, X $ \setminus ∅ = X $ (himpunan seluruhnya), merupakan himpunan terbuka. Jadi, himpunan kosong bersifat terbuka dan tertutup sekaligus. - Himpunan seluruhnya (X)
Himpunan seluruhnya juga selalu terbuka secara definisi. Ia tertutup karena komplemennya, $ X \setminus X = ∅ $ (himpunan kosong), adalah himpunan terbuka. Maka, himpunan seluruhnya pun merupakan himpunan clopen.
Kesimpulannya, dalam setiap topologi, dua himpunan ini - himpunan kosong dan himpunan seluruhnya - selalu bersifat clopen. Konsep ini menjadi dasar penting dalam memahami bagaimana struktur topologi dibangun.