Transformasi Topologi

Transformasi topologi adalah operasi pada ruang topologi yang mempertahankan sifat-sifat mendasar seperti keterhubungan dan kontinuitas.

Transformasi ini memegang peranan sentral dalam topologi, cabang matematika yang meneliti sifat-sifat ruang yang tetap tidak berubah di bawah transformasi kontinu.

Ciri utama transformasi topologi mencakup hal-hal berikut:

• Kontinuitas
  Transformasi topologi harus kontinu, artinya perubahan kecil pada input menghasilkan perubahan kecil pula pada output.
• Keterhubungan dan Kedekatan
  Transformasi topologi menjaga konsep kedekatan dan keterhubungan. Jika dua titik berdekatan atau terhubung dalam ruang asal, maka sifat itu akan tetap terjaga dalam ruang hasil transformasi.
• Deformasi tanpa robekan atau penempelan
  Objek dapat diregangkan, ditekan, atau dibengkokkan, tetapi tidak boleh dirobek atau direkatkan kembali. Misalnya, donat dapat diubah menjadi cangkir kopi melalui transformasi topologi karena keduanya sama-sama memiliki satu "lubang."

Penerapan: Transformasi topologi digunakan di berbagai bidang, mulai dari matematika murni seperti teori simpul dan topologi aljabar, untuk mengkaji sifat-sifat objek yang tetap tidak berubah di bawah deformasi kontinu.

Jenis-jenis Transformasi Topologi

Dalam topologi, transformasi biasanya diklasifikasikan berdasarkan sifat topologi yang mereka pertahankan.

Beberapa jenis transformasi topologi yang mendasar adalah sebagai berikut:

• Homeomorfisme
  Homeomorfisme adalah transformasi kontinu dengan invers yang juga kontinu. Artinya, suatu ruang dapat diubah menjadi ruang lain, lalu dikembalikan lagi tanpa proses "merobek" atau "merekatkan." Konsep ini mendasari banyak hal dalam topologi. Contohnya, perubahan bentuk cangkir menjadi donat.
• Isotopi
  Isotopi adalah kasus khusus homeomorfisme, di mana setiap tahap transformasi juga merupakan homeomorfisme. Misalnya, menggeser simpul pada seutas tali tanpa mengencangkan atau melonggarkannya; setiap tahap pergeseran merupakan isotopi.
• Homotopi
  Homotopi menunjukkan bagaimana sebuah fungsi dapat "dideformasi" menjadi fungsi lain sambil mempertahankan sifat topologi tertentu. Homotopi lebih longgar syaratnya dibanding homeomorfisme. Contohnya, peregangan pegas dan pelepasannya kembali; bentuk-bentuk yang muncul selama proses itu bersifat homotopik.
• Diffeomorfisme
  Diffeomorfisme adalah homeomorfisme yang juga terdiferensialkan. Konsep ini penting dalam topologi diferensial, di mana kelicinan dan sifat terdiferensialkan permukaan sangat relevan. Misalnya, mengubah bola elastis menjadi elipsoid memanjang.

Jenis-jenis transformasi ini menyoroti aspek yang berbeda dari kontinuitas dan kemampuan deformasi ruang maupun fungsi dalam topologi.

Penerapannya bervariasi sesuai konteks, baik dalam topologi umum, topologi aljabar, maupun topologi diferensial.

Perbedaan Transformasi Geometri dan Topologi

Transformasi geometri dan transformasi topologi berbeda dari segi sifat maupun penerapannya:

• Transformasi Geometri
  Transformasi geometri mengubah objek dalam ruang sambil mempertahankan sifat geometri seperti jarak, sudut, dan bentuk. Contoh: translasi, rotasi, refleksi, dan dilatasi.

  Sebagai contoh, rotasi mempertahankan jarak dan sudut, tetapi mengubah orientasi.

• Transformasi Topologi
  Transformasi topologi mengubah ruang sambil mempertahankan sifat topologi seperti keterhubungan dan kontinuitas, tetapi tidak harus menjaga jarak atau sudut. Transformasi ini jauh lebih fleksibel, memungkinkan peregangan dan deformasi tanpa robekan atau penempelan.

  Sebagai contoh, topologi memungkinkan donat diubah menjadi cangkir kopi karena keduanya memiliki satu lubang.

Sementara transformasi geometri berfokus pada perpindahan atau perubahan bentuk dengan tetap menjaga ukuran dan proporsi tertentu, transformasi topologi menekankan deformasi ruang yang mempertahankan keterhubungan dan kontinuitas, tanpa memperhatikan bentuk atau ukuran yang persis.

Apakah sebuah transformasi bisa bersifat sekaligus geometri dan topologi?

Ya, ada transformasi yang tidak hanya mempertahankan sifat geometri seperti sudut, panjang, dan bentuk, tetapi juga kontinu serta menjaga sifat topologi seperti keterhubungan dan kontinuitas.

Beberapa contoh praktis:

• Isometri
  Isometri, seperti translasi, rotasi, dan refleksi, mempertahankan jarak antar titik dan sudut, sehingga termasuk transformasi geometri sekaligus topologi. Transformasi ini juga merupakan homeomorfisme karena memiliki invers yang kontinu.
  
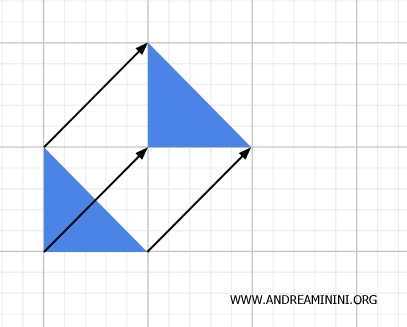
• Kesebangunan
  Kesebangunan mengubah ukuran objek tetapi mempertahankan bentuk, termasuk dilatasi atau kontraksi yang menjaga sudut dan perbandingan relatif. Transformasi ini bersifat geometri karena mengubah ukuran, sekaligus topologi karena kontinu dan tetap menjaga keterhubungan.

Contoh-contoh ini menunjukkan bahwa sifat geometri dan topologi tidak selalu terpisah. Dalam beberapa kasus, sebuah transformasi dapat sekaligus bermakna secara geometri dan sah secara topologi.

Dan seterusnya.