Bola Terbuka

Dalam topologi, bola terbuka adalah himpunan semua titik yang berjarak kurang dari suatu nilai tertentu dari satu titik pusat (c). Nilai ini disebut jari-jari (r). Dengan kata lain, bola terbuka mencakup semua titik yang “cukup dekat” dengan pusatnya, sejauh jarak tersebut lebih kecil dari r. $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Konsep ini didefinisikan dalam ruang metrik (\( M \)), yaitu ruang di mana jarak antara dua titik diukur dengan suatu fungsi yang disebut metrik. Metrik berperan penting untuk menentukan seberapa jauh satu titik dari titik lainnya.

Bola terbuka sepenuhnya ditentukan oleh pusat dan jari-jarinya. Kedua unsur ini menentukan bentuk dan ukuran wilayah yang dimaksud.

Disebut “terbuka” karena, dalam pengertian topologis, di dalam setiap bola terbuka selalu dapat ditemukan bola terbuka lain yang lebih kecil dan sepenuhnya berada di dalamnya. Sifat inilah yang menjadikan bola terbuka konsep dasar dalam topologi.

Catatan: Bola terbuka tidak berubah jika digeser (translasi) atau diperbesar maupun diperkecil (penskalaan). Artinya, mengubah posisi atau ukurannya tidak memengaruhi sifat dasarnya sebagai bola terbuka.

Contohnya pada bidang R². Di sini digunakan metrik Euclidean untuk menghitung jarak antara titik p=(x,y) dan titik pusat c=(x₀,y₀).

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

Lingkungan melingkar terbuka seperti ini memiliki peran penting dalam menentukan struktur topologi pada bidang, dan menjadi dasar pembentukan suatu sistem topologis yang lengkap.

Topologi standar pada bidang R² dibangun dari kumpulan seluruh bola terbuka seperti ini.

$$ B = \{ B(p, r) \ | \ p \in R^2, \ r > 0 \} $$

Dalam hal ini, p menyatakan titik p=(x,y) pada ruang dua dimensi, sedangkan r menunjukkan jari-jari dari lingkungan melingkar tersebut.

Meskipun bukan satu-satunya topologi yang dapat digunakan pada bidang, topologi ini adalah yang paling umum dan sering dijadikan acuan.

Pada setiap bola terbuka, setiap titik $ q \in B(p,r) $ juga dapat menjadi pusat dari bola terbuka yang lebih kecil, B(q,ε), yang seluruhnya berada di dalam bola semula B(p,r).

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ sehingga \ B(q,ε) \subset B(p,r) $$

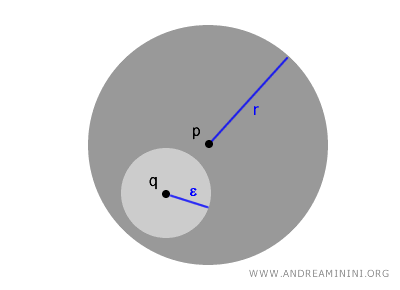
Sifat ini menunjukkan bagaimana struktur ruang metrik tersusun secara berlapis dan tak terbatas, di mana setiap titik memiliki “ruang” tersendiri di dalam ruang yang lebih besar.