Himpunan Terbuka
Sebuah himpunan A disebut himpunan terbuka jika untuk setiap elemen x di dalamnya (x∈A), terdapat suatu lingkungan (neighborhood) yang seluruhnya masih berada di dalam himpunan tersebut.
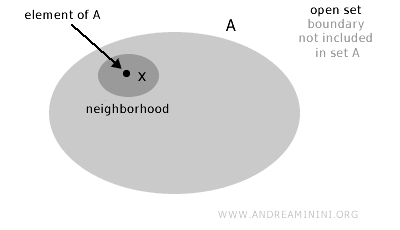
Dengan kata lain, suatu himpunan dikatakan terbuka apabila, secara intuitif, "batas-batasnya" tidak termasuk dalam himpunan itu sendiri.
Secara formal, himpunan A dalam ruang topologi X disebut terbuka jika untuk setiap titik x di A terdapat lingkungan dari x yang sepenuhnya terkandung di dalam A.
Catatan. Ini berarti bahwa di sekitar setiap titik dalam himpunan, selalu dapat ditemukan suatu "wilayah" yang sepenuhnya berada di dalam himpunan tersebut tanpa "menyentuh" batas luarnya.
Contoh Praktis
Contoh sederhana dari himpunan terbuka pada garis bilangan adalah interval terbuka.
Apa itu interval terbuka (open interval)? Interval terbuka pada \( \mathbb{R} \) adalah himpunan semua bilangan real \( x \) yang memenuhi \( a < x < b \), dengan \( a \) dan \( b \) bilangan real serta \( a < b \).
Interval ini dilambangkan dengan (a,b), di mana tanda kurung bulat menunjukkan bahwa titik ujung a dan b tidak termasuk dalam himpunan.
Misalnya, interval terbuka (3,10) merupakan himpunan terbuka pada garis bilangan real.
Dalam kasus ini, himpunan A terdiri dari tak terhitung banyak bilangan antara 3 dan 10, tanpa menyertakan kedua ujungnya.
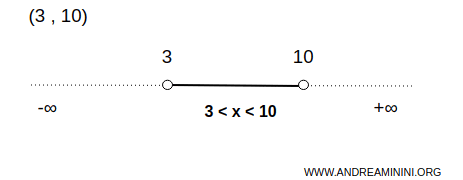
Artinya, untuk setiap titik x di dalam interval tersebut, selalu ada interval terbuka kecil di sekitar x yang sepenuhnya berada di dalam (3,10).
Misalnya, untuk titik x=3.1, kita dapat mengambil interval (3.09,3.11) yang sepenuhnya berada di dalam (3,10).
Hal yang sama berlaku bagi setiap titik lain di dalam (3,10), karena antara dua bilangan real mana pun selalu terdapat tak terhingga banyak bilangan real di antaranya.
Catatan. Bahkan jika kita mengambil bilangan real yang sangat dekat dengan salah satu ujung, misalnya 3.001, kita masih dapat membuat lingkungan 3.001±0.00000001 yang berisi tak terhingga banyak bilangan real di dalam interval terbuka (3,10).
Ini merupakan contoh satu dimensi yang sederhana dari himpunan terbuka.
Contoh Lain
Konsep ini dapat diperluas ke ruang dua dimensi, misalnya bidang koordinat.
Pertimbangkan himpunan titik-titik di dalam lingkaran dengan jari-jari r=1 dan berpusat di titik asal (0;0):
$$ x^2+y^2<1 $$
Pertidaksamaan ini menggambarkan himpunan semua titik yang jaraknya dari pusat (0,0) kurang dari 1. Dengan demikian, titik-titik pada keliling tidak termasuk, hanya titik-titik di bagian dalam lingkaran.
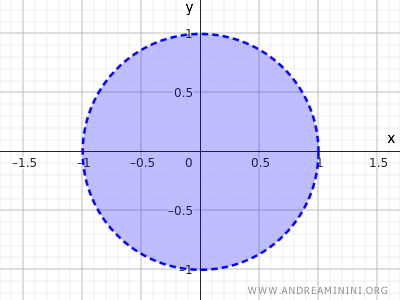
Ini adalah contoh lain dari himpunan terbuka.
Kapan suatu himpunan disebut tertutup?
Untuk mendapatkan himpunan tertutup, cukup tambahkan titik-titik pada keliling ke dalam himpunan.
$$ x^2+y^2 \le 1 $$
Pada kasus ini, syarat bahwa setiap titik memiliki lingkungan yang seluruhnya berada di dalam himpunan tidak lagi berlaku.
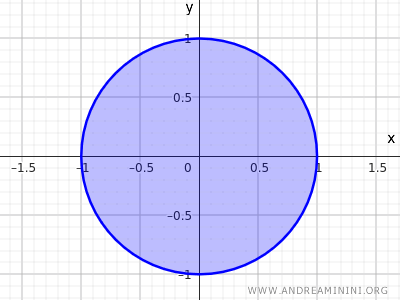
Pada himpunan tertutup, titik-titik pada keliling tidak memiliki lingkungan yang sepenuhnya berada di dalam himpunan.
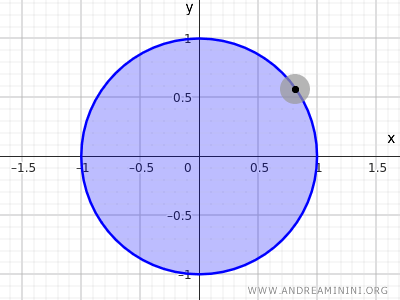
Catatan. Dalam topologi, persamaan lingkaran $ x^2+y^2=1 $ bukanlah himpunan terbuka maupun tertutup di ruang Euclidean R2, karena hanya mencakup titik-titik pada keliling tanpa bagian dalamnya. Sebaliknya, himpunan titik-titik yang didefinisikan oleh $ x^2+y^2<1 $, yang mencakup bagian dalam tetapi tidak kelilingnya, adalah contoh himpunan terbuka. Jika kita juga menyertakan kelilingnya, $ x^2+y^2\le 1 $, hasilnya adalah himpunan tertutup.
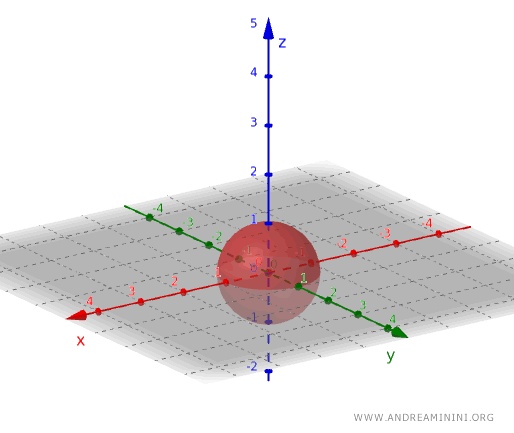
Dengan prinsip yang sama, himpunan terbuka dalam ruang tiga dimensi dapat diperoleh, misalnya, dengan mempertimbangkan himpunan titik-titik di dalam bola tetapi tidak termasuk permukaannya.
Memilih Topologi
Interval terbuka sangat berguna karena mudah dipahami dan memberikan gambaran intuitif tentang apa itu himpunan terbuka.
Namun, konsep himpunan terbuka sebenarnya lebih luas dan tidak terbatas hanya pada interval terbuka.
Oleh karena itu, setelah memahami konsep dasarnya, penting untuk mempelajarinya secara lebih mendalam.
Konsep "terbuka" pada suatu himpunan bergantung pada topologi yang diterapkan pada ruang tersebut.
Hal penting yang perlu dipahami adalah bahwa definisi himpunan terbuka dapat berbeda-beda tergantung topologi yang digunakan pada ruang itu.
Dalam beberapa ruang, sebuah himpunan yang tampak "tertutup" dalam topologi biasa bisa saja dianggap "terbuka" dalam topologi yang lain.
Dengan kata lain, suatu himpunan dapat dianggap terbuka tergantung pada topologi yang didefinisikan pada ruangnya.
Apa itu topologi? Topologi pada suatu ruang pada dasarnya adalah kumpulan himpunan yang dianggap "terbuka" menurut aturan tertentu, misalnya gabungan sebarang himpunan terbuka tetap merupakan himpunan terbuka, dan perpotongan sejumlah terbatas himpunan terbuka juga merupakan himpunan terbuka.
Karena itu, sebaiknya kita tidak membatasi pemahaman hanya pada contoh yang paling umum dan mudah dibayangkan seperti interval atau cakram terbuka.
Dalam topologi, definisi "himpunan terbuka" jauh lebih luas dan dapat mencakup himpunan-himpunan yang pada pandangan pertama mungkin tidak terlihat sebagai himpunan terbuka.
Contoh Praktis
Pertimbangkan ruang \( \{a, b\} \) yang hanya memiliki dua elemen.
Dalam ruang ini, setidaknya terdapat dua topologi yang dapat didefinisikan: topologi trivial dan topologi diskret.
- Topologi Trivial
Dalam topologi trivial pada \( \{a, b\} \), satu-satunya himpunan terbuka adalah himpunan kosong \( \emptyset \) dan ruang itu sendiri \( \{a, b\} \). Ini merupakan topologi paling sederhana, yang hampir tidak memiliki struktur "terbuka" selain ruang penuh dan himpunan kosong. - Topologi Diskret
Dalam topologi diskret, setiap himpunan bagian dari \( \{a, b\} \) dianggap terbuka. Artinya, \( \{a\} \), \( \{b\} \), \( \{a, b\} \), dan \( \emptyset \) semuanya merupakan himpunan terbuka. Topologi diskret adalah yang paling "kaya" karena setiap kombinasi titik menghasilkan himpunan terbuka.
Sekarang perhatikan himpunan \( \{a\} \) pada kedua topologi tersebut:
- Pada topologi trivial, himpunan {a} tidak terbuka
Satu-satunya himpunan terbuka yang berisi elemen adalah \( \{a, b\} \), selain himpunan kosong. - Pada topologi diskret, himpunan {a} adalah terbuka
Dalam topologi ini, setiap himpunan bagian dari \( \{a, b\} \), termasuk \( \{a\} \) dan \( \{b\} \), didefinisikan sebagai himpunan terbuka.
Dengan demikian, himpunan \( \{a\} \) merupakan himpunan terbuka dalam topologi diskret, tetapi tidak dalam topologi trivial.
Contoh sederhana ini menunjukkan bahwa pengertian himpunan terbuka sangat bergantung pada topologi yang digunakan.
Teorema tentang Himpunan Terbuka
Teorema 1
Diberikan sebuah himpunan terbuka X dan topologi T yang bersama-sama membentuk ruang topologi (X,T), maka suatu himpunan bagian S⊂X disebut himpunan terbuka dalam ruang topologi (X,T) apabila setiap elemen (atau titik) s∈S memiliki sebuah lingkungan U yang sepenuhnya berada di dalam S, artinya U⊂S.
Menurut definisi, S adalah himpunan terbuka karena merupakan bagian dari ruang topologi (X,T).
Dengan demikian, himpunan bagian S dapat dipandang sebagai lingkungan bagi setiap titiknya s∈S.
Dari hal ini dapat disimpulkan bahwa lingkungan Us untuk setiap elemen s∈S merupakan himpunan terbuka yang terkandung di dalam S.
$$ x \in U_s \subset S \subset X $$
Himpunan terbuka dapat dipandang sebagai gabungan dari lingkungan terbuka bagi setiap titik di dalamnya.
Oleh karena itu, jika setiap elemen s∈S dari suatu himpunan bagian S memiliki lingkungan Us⊂S yang seluruhnya terkandung dalam S, maka dapat disimpulkan bahwa S adalah himpunan terbuka karena merupakan gabungan dari himpunan-himpunan terbuka.
Dengan kata lain, suatu himpunan disebut terbuka jika dan hanya jika untuk setiap titik di dalamnya terdapat lingkungan dari titik tersebut yang seluruhnya berada di dalam himpunan tersebut.
Contoh. Bayangkan sebuah meja yang di atasnya tersebar banyak kelereng kaca. Setiap kelereng mewakili satu titik dalam suatu himpunan. Mengatakan bahwa himpunan ini "terbuka" berarti di sekitar setiap kelereng ada cukup ruang untuk bergerak bebas tanpa keluar dari tepi meja. Jika untuk setiap kelereng di meja ini kita dapat menggambar lingkaran di sekitarnya yang seluruhnya berada di atas meja (tanpa menyentuh tepi), maka himpunan kelereng di meja tersebut merupakan "himpunan terbuka". Dengan kata lain, keterbukaan himpunan berarti bahwa, untuk kelereng mana pun yang dipilih, selalu ada "ruang bebas" di sekitarnya yang masih termasuk dalam himpunan tersebut.

Teorema 2
Misalkan terdapat himpunan \( X \) dan sebuah basis \( B \) untuk suatu topologi pada \( X \). Himpunan bagian \( A \subset X \) disebut terbuka dalam topologi yang dibangkitkan oleh \( B \) jika dan hanya jika, untuk setiap elemen \( x \) di dalam \( A \), terdapat elemen basis \( B_x \in B \) sehingga \( x \in B_x \) dan \( B_x \subseteq A \).
Teorema ini menyoroti ciri penting dari topologi yang dibangun melalui sebuah basis.
Secara sederhana, setiap titik dalam himpunan terbuka \( A \) harus memiliki sebuah "lingkungan" \( B_x \) yang berasal dari himpunan basis dan sepenuhnya berada di dalam \( A \).
Hal ini memastikan bahwa himpunan \( A \) benar-benar terbuka dalam topologi yang dihasilkan oleh \( B \).
Bukti. Jika A adalah himpunan terbuka dalam topologi yang dibangkitkan oleh basis B pada himpunan X, di mana A merupakan himpunan bagian dari X, maka secara definisi A merupakan gabungan dari elemen-elemen basis. Artinya, setiap elemen x di A berada di dalam setidaknya satu elemen basis Bx, dan Bx tersebut sepenuhnya terkandung di dalam A. Karena A adalah gabungan dari elemen-elemen basis, maka Bx ⊂ A. Sebaliknya, jika untuk setiap x di A terdapat elemen basis Bx yang seluruhnya terkandung di dalam A, maka A adalah himpunan terbuka dalam topologi yang dihasilkan oleh B.
Contoh
Pertimbangkan himpunan \( X = \{1, 2, 3, 4, 5\} \) dengan basis topologi \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). Kita ingin menentukan apakah himpunan \( A = \{1, 2, 3\} \) merupakan himpunan terbuka.
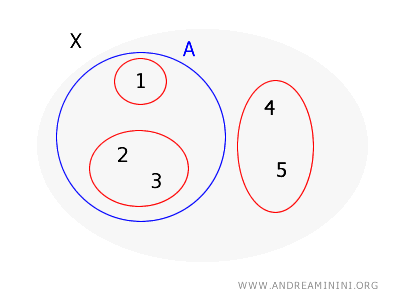
Untuk setiap titik dalam \( A \), kita perlu menemukan elemen basis yang mengandung titik tersebut dan sepenuhnya berada di dalam \( A \):
- Untuk titik \( 1 \) dalam \( A \), terdapat elemen basis \( \{1\} \) yang memuat \( 1 \) dan sepenuhnya berada di dalam \( A \).
- Untuk titik \( 2 \) dalam \( A \), elemen basis \( \{2, 3\} \) memuat \( 2 \) dan sepenuhnya berada di dalam \( A \).
- Untuk titik \( 3 \) dalam \( A \), elemen basis yang sama \( \{2, 3\} \) juga memuat \( 3 \) dan sepenuhnya berada di dalam \( A \).
Setiap titik dalam \( A \) termasuk dalam suatu elemen basis yang seluruhnya berada di dalam \( A \), sehingga memenuhi syarat teorema.
Maka dapat disimpulkan bahwa \( A \) adalah himpunan terbuka dalam topologi yang dihasilkan oleh basis \( B \).
Contoh 2
Pertimbangkan kembali himpunan \( X = \{1, 2, 3, 4, 5\} \) dengan basis topologi yang sama, \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \).
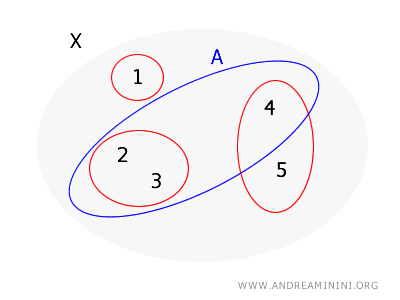
Kali ini, kita ingin memeriksa apakah himpunan \( A = \{2, 3, 4\} \) merupakan himpunan terbuka.
- Untuk titik \( 2 \), terdapat elemen basis \( \{2, 3\} \) yang sepenuhnya berada di dalam \( A \).
- Untuk titik \( 3 \), elemen basis yang sama \( \{2, 3\} \) juga sepenuhnya berada di dalam \( A \).
- Namun untuk titik \( 4 \), tidak ada elemen basis yang mengandungnya dan sepenuhnya berada di dalam \( A \), karena satu-satunya elemen basis yang memuat 4 adalah \( \{4, 5\} \), yang tidak seluruhnya berada di dalam \( A \) (karena memuat 5 yang tidak termasuk dalam \( A \)).
Oleh karena itu, menurut teorema ini, himpunan \( A \) bukan himpunan terbuka dalam topologi yang dibangkitkan oleh basis \( B \), karena tidak setiap titik di dalam \( A \) memiliki elemen basis yang sepenuhnya berada di dalam \( A \).
Catatan Tambahan
Beberapa catatan tambahan mengenai himpunan terbuka:
- Suatu himpunan A terbuka jika dan hanya jika A = Int(A)
Himpunan \( A \) dalam ruang topologi \( X \) disebut terbuka jika sama dengan interior-nya sendiri. Interior dari suatu himpunan, dilambangkan dengan Int(A), adalah gabungan dari semua himpunan terbuka yang terkandung di dalam \( A \). $$ A = \text{Int}(A) $$
Dan seterusnya.