Ruang Terhubung Jalur
Sebuah ruang topologi S disebut terhubung jalur apabila terdapat suatu jalur kontinu yang menghubungkan setiap pasangan titik A dan B di dalam ruang tersebut, tanpa harus keluar dari ruang itu sendiri.
Bayangkan selembar kertas tanpa memperhitungkan sisi-sisinya.
Kertas itu merepresentasikan suatu area kontinu dan dipandang sebagai ruang terbuka karena batasnya tidak termasuk.
Di dalamnya, untuk setiap titik A dan B, kita dapat menggambar sebuah garis dengan pena tanpa pernah mengangkatnya dari kertas.
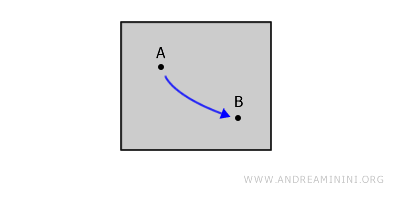
Dengan kata lain, jalur tersebut sepenuhnya berada di dalam ruang yang memuat titik A dan B.
Setiap ruang yang terhubung jalur pasti merupakan ruang yang terhubung.
Hal ini cukup intuitif; jika sebuah ruang tidak terhubung, maka ia akan terpecah menjadi bagian-bagian terpisah sehingga tidak ada jalur kontinu yang bisa menghubungkan sepasang titik tanpa keluar dari ruang tersebut.
Namun, pernyataan sebaliknya tidak selalu benar. Tidak semua ruang yang terhubung merupakan ruang terhubung jalur.
Pertimbangkan ilustrasi berikut, yang meskipun tampak berlawanan dengan intuisi, secara matematis memang mungkin.
Misalkan kita ambil dua himpunan, Q dan T:
$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$
$$ T = \{ \ 0 \} $$
Himpunan pertama, Q, terdiri atas semua titik pada grafik gelombang sinus yang terdefinisi untuk setiap bilangan real R, kecuali nol. Pada titik nol fungsi tidak terdefinisi karena terjadi pembagian dengan nol.
Himpunan kedua, T, hanya berisi titik nol itu sendiri.
Kedua himpunan, Q dan T, saling mendekati tanpa batas, sebagaimana terlihat pada grafik fungsi kontinu sin(1/x).
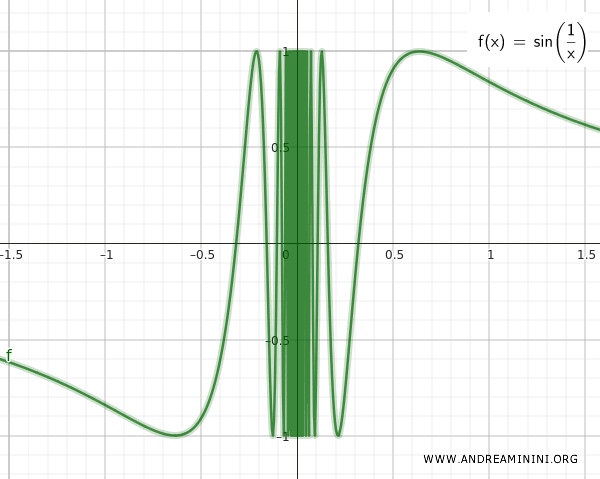
Kemudian kita bentuk himpunan S sebagai gabungan Q dan T:
$$ S = Q \cup T $$
Himpunan S terhubung karena untuk setiap ε>0 selalu ada lingkungan di sekitar nol (0-ε, 0+ε) yang memuat titik-titik dari Q.
Hal ini terjadi karena nol merupakan titik akumulasi dari fungsi sin(1/x).
Namun demikian, S tidak terhubung jalur karena tidak ada kurva kontinu yang dapat menghubungkan titik mana pun dari Q dengan titik nol (himpunan T).
Catatan: Situasinya akan berbeda apabila fungsi yang digunakan adalah f(x)=1/x. Dalam kasus tersebut jelas bahwa himpunan Q dan T terpisah sama sekali, tidak saling mendekat.
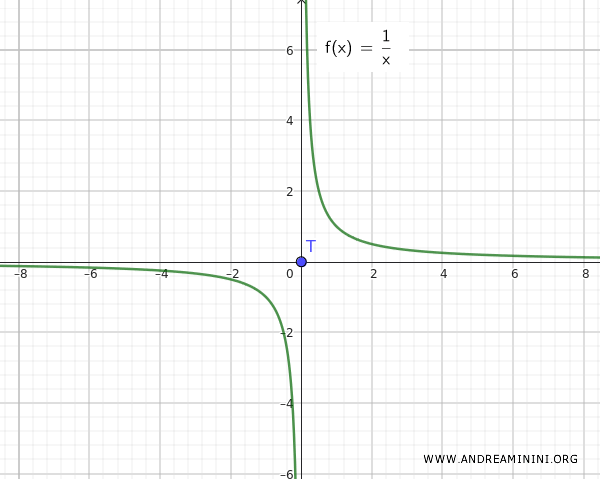
Contoh ini menunjukkan bahwa gabungan sebuah himpunan terhubung Q={∀ x ∈ R-{0}, 1/x} dengan sebuah titik terisolasi T={0} tidak serta merta menghasilkan himpunan terhubung, kecuali titik terisolasi itu (misalnya nol) juga merupakan titik akumulasi.
Dan seterusnya.