Memahami Ruang Simply Connected dalam Topologi

Simply connected adalah istilah dalam topologi yang berarti: setiap lintasan tertutup di dalam suatu ruang bisa “dipadatkan” atau dideformasi secara kontinu hingga menyusut menjadi satu titik.

Dengan kata lain, jika kita membuat sebuah loop di dalam ruang itu, loop tersebut selalu bisa ditarik hingga menjadi titik tanpa harus keluar dari ruang tersebut.

Artinya, ruang simply connected bersifat utuh, tidak terpecah-pecah, dan tidak memiliki “lubang” di dalamnya.

Catatan penting: setiap ruang simply connected sudah pasti connected (terhubung). Namun, tidak semua ruang terhubung bisa disebut simply connected.

Contoh yang Mudah Dipahami

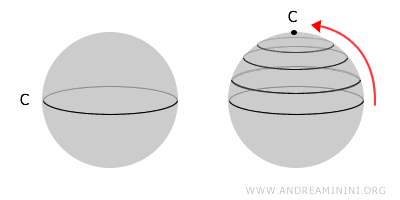
Bayangkan sebuah bola (sphere). Bola adalah contoh ruang simply connected: kurva tertutup apa pun yang kita gambar di permukaannya bisa ditarik menyusut hingga menjadi satu titik.

Lain halnya dengan torus-atau bentuk donat. Torus bukan simply connected karena adanya lubang di tengah. Lubang ini membuat sebagian loop tidak bisa diciutkan menjadi titik.

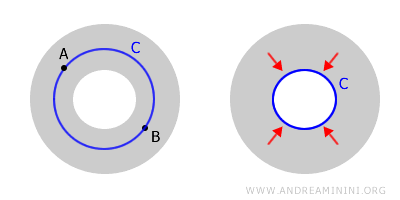
Dari sini kita bisa melihat: sekadar terhubung (connected) tidak otomatis berarti simply connected.

Donat tetap termasuk ruang terhubung, karena setiap dua titik di permukaannya bisa dihubungkan dengan sebuah lintasan yang seluruhnya berada di dalam ruang tersebut. Tetapi donat tidak simply connected, sebab tidak semua kurva tertutup di dalamnya bisa dipadatkan menjadi satu titik.

Ruang yang terhubung tetapi tidak simply connected disebut multiply connected space. Contoh klasiknya adalah cincin (annulus) dan torus.

Kesimpulan

Secara singkat: syarat simply connected lebih ketat daripada sekadar keterhubungan melalui lintasan. Ruang yang simply connected selalu terhubung, tapi tidak semua ruang terhubung bersifat simply connected.

Konsep ini penting dalam topologi karena membantu kita membedakan antara ruang yang benar-benar “utuh” dengan ruang yang punya struktur lebih kompleks, seperti adanya lubang atau jalan melingkar yang tidak bisa dipadatkan.