Himpunan yang Bukan Terbuka dan Bukan Tertutup
Dalam topologi, ada himpunan yang tidak dapat digolongkan sebagai himpunan terbuka maupun himpunan tertutup karena tidak memenuhi kriteria salah satu di antaranya.
Kondisi seperti ini muncul ketika suatu himpunan tidak terdaftar sebagai himpunan terbuka (open set) dan pada saat yang sama bukan merupakan komplemen dari himpunan terbuka apa pun dalam topologi tersebut.
Akibatnya, himpunan tersebut juga tidak dapat disebut sebagai himpunan tertutup (closed set).
Catatan: Dalam topologi bilangan real yang umum dipelajari, kasus seperti ini jarang muncul sehingga sulit dibayangkan secara intuitif. Namun, dalam topologi yang lebih umum, situasi ini sepenuhnya mungkin terjadi. Sebuah contoh konkret akan membantu memperjelas gagasannya.
Contoh
Pertimbangkan himpunan X={a,b,c,d} dengan topologi T yang mendefinisikan himpunan-himpunan terbuka berikut: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d}, dan Ø.
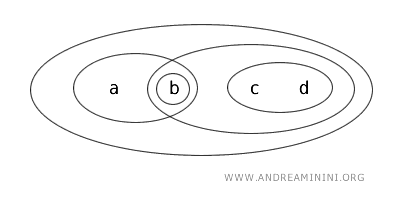
Amati sekarang subset {b,c} dari himpunan X.
- Himpunan {b,c} bukan "himpunan terbuka" karena tidak tercantum dalam daftar himpunan terbuka yang didefinisikan oleh topologi T.
- Himpunan {b,c} juga bukan komplemen dari himpunan terbuka mana pun dalam topologi T, sehingga tidak dapat digolongkan sebagai "himpunan tertutup".
Berdasarkan topologi T, dapat disimpulkan bahwa himpunan {b,c} bukan himpunan terbuka dan bukan pula himpunan tertutup. Contoh ini menunjukkan bahwa dalam topologi, tidak semua himpunan harus masuk ke salah satu dari dua kategori tersebut. Masih banyak sifat menarik lain yang muncul dalam studi topologi, dan pemahaman konsep ini menjadi langkah penting untuk mempelajarinya lebih jauh.