Topologi

Topologi adalah cabang matematika yang mempelajari sifat-sifat ruang yang tetap tidak berubah ketika ruang tersebut mengalami deformasi kontinu, seperti diregangkan, dibengkokkan, atau dipelintir, selama tidak terjadi penyobekan maupun pengeleman.

Intinya, topologi berurusan dengan sifat-sifat geometris yang bertahan di bawah transformasi kontinu.

Sifat-sifat ini hanya dapat berubah melalui proses yang tidak kontinu, misalnya ketika suatu bagian ruang disobek atau ketika dua bagian ruang yang terpisah disatukan.

Sebagai ilustrasi, sebuah bola dan sebuah kubus dianggap ekuivalen secara topologis, karena keduanya dapat diubah satu sama lain melalui deformasi kontinu tanpa perlu menyobek atau menempelkan.

Sebaliknya, sebuah bola dan sebuah torus tidak ekuivalen secara topologis, karena mengubah yang satu menjadi yang lain mengharuskan adanya penciptaan atau penghilangan sebuah lubang, yang pada akhirnya selalu melibatkan penyobekan atau pengeleman.

Dengan kata lain, topologi menekankan cara ruang disusun dan bagaimana bagian-bagiannya saling terhubung, bukan ukuran yang presisi seperti jarak, besar, atau bentuk.

Dalam sudut pandang topologi, konsep seperti panjang, luas, volume, atau sudut tidak menjadi perhatian utama. Yang penting adalah sifat-sifat kualitatif suatu bentuk dan kemungkinan untuk mengubahnya menjadi bentuk lain melalui deformasi kontinu.

Pendekatan ini mencakup berbagai gagasan penting, seperti keterhubungan, kekompakan, jumlah lubang pada suatu objek, serta sifat-sifat global lain dari sebuah ruang.

Topologi juga memperkenalkan konsep ruang topologis, dengan transformasi kunci berupa homeomorfisme, yaitu pemetaan yang kontinu dan dapat dibalik, yang mengubah suatu ruang sambil tetap mempertahankan struktur topologisnya.

Karena itu, topologi sering dijuluki sebagai “geometri lembaran karet”. Objek dibayangkan terbuat dari bahan elastis yang dapat diregangkan, dibengkokkan, atau dikompresi, tetapi tidak boleh disobek atau ditempelkan. Bidang ini merupakan salah satu fondasi penting sekaligus sangat menyatukan dalam matematika modern.

Sejarah

Perkembangan topologi dimulai pada abad ke-18.

Akar awalnya dapat ditelusuri pada masalah Tujuh Jembatan Königsberg karya Leonhard Euler, yang memperkenalkan konsep dasar keterhubungan dan teori jaringan.

Masalah ini memicu pertanyaan mendasar tentang sifat-sifat ruang, dan menjadi landasan bagi lahirnya bidang topologi.

Masalah Tujuh Jembatan: Di sebuah pulau sungai terdapat tujuh jembatan. Dari titik awal manapun, rute apa yang memungkinkan seseorang menyeberangi setiap jembatan tepat satu kali? Syarat pentingnya: tidak boleh menyeberangi jembatan yang sama lebih dari sekali.

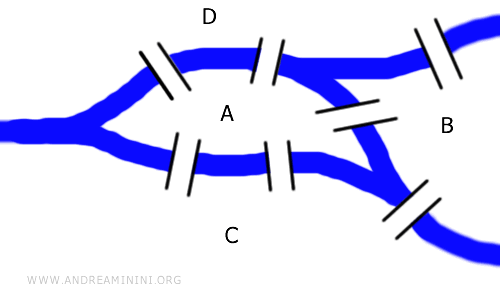
Tantangan ini tidak membutuhkan informasi jarak atau panjang jembatan; masalah ini sepenuhnya bersifat topologis dan dapat juga direpresentasikan dengan graf. Graf di bawah ini secara topologis ekuivalen dengan tata letak jembatan asli.

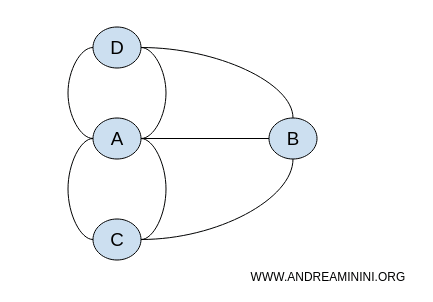
Posisi spesifik simpul dalam graf tidak penting. Yang terpenting adalah hubungan antar simpul. Karena itu, masalah ini dapat digambarkan dengan jumlah graf yang tak terbatas tetapi tetap ekuivalen secara topologis.

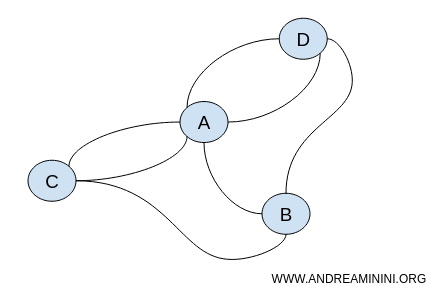
Kedua graf mempertahankan sifat topologis yang sama, seperti kontinuitas dan keterhubungan.

Euler menyadari bahwa masalah Tujuh Jembatan Königsberg, meski bersifat geometris, tidak bergantung pada pengukuran ukuran.

Ia menunjukkan bahwa masalah tersebut pada dasarnya tentang posisi, dan membuktikan bahwa masalah itu tidak dapat diselesaikan, sehingga melahirkan gagasan tentang "geometri posisi."

Sepanjang abad ke-19, matematikawan seperti Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann, dan Felix Klein meneliti sifat bentuk dan permukaan, memperluas pemahaman kita tentang sifat-sifat topologi.

Catatan: Johann Listing pertama kali memperkenalkan istilah "topologi" pada tahun 1847, meski baru diakui luas dalam komunitas ilmiah beberapa dekade kemudian.

Pada abad ke-19, geometri posisi menemukan penerapan praktis dalam bidang seperti analisis jaringan listrik oleh Gustav Kirchhoff.

Selanjutnya, Henri Poincaré pada akhir abad ke-19 dan awal abad ke-20 memberikan kontribusi besar terhadap geometri posisi lewat karyanya dalam topologi aljabar.

Pada abad ke-20, topologi bercabang ke bidang khusus seperti topologi aljabar dan topologi umum, dengan kontribusi besar dari matematikawan seperti Felix Hausdorff, Cantor, dan Brouwer, khususnya dalam matematika abstrak.

Saat ini, topologi telah menjadi cabang penting matematika yang berfokus pada sifat-sifat yang tidak berubah di bawah transformasi kontinu.

Topologi kini mencakup berbagai sub-disiplin, masing-masing memusatkan perhatian pada aspek yang berbeda dari ruang topologi, termasuk topologi aljabar, topologi diferensial, topologi umum, dan topologi geometris.

Secara keseluruhan, topologi dapat dipandang sebagai studi umum tentang bentuk sekaligus sebagai disiplin matematika abstrak.

Meski bersifat abstrak, konsep-konsep topologi memiliki banyak penerapan nyata di berbagai bidang seperti ekonomi, teknik, dan sains.

Ruang Topologi

Ruang topologi adalah himpunan X yang dilengkapi dengan struktur T yang disebut "topologi," yang menyediakan kerangka untuk memahami konsep abstrak seperti kontinuitas, kedekatan, dan limit secara lebih umum dibandingkan geometri atau analisis tradisional.

$$ (X,T) $$

Contoh: Contoh klasik ruang topologi adalah garis bilangan real \( \mathbb{R} \) dengan topologi standarnya, di mana suatu himpunan dianggap terbuka jika mencakup interval di sekitar setiap titik. Struktur ini memudahkan kajian konsep seperti kontinuitas dan limit dari perspektif topologi.

Homeomorfisme

Homeomorfisme adalah transformasi bijektif dan kontinu antara dua ruang topologi, dengan invers yang juga kontinu, sehingga sifat-sifat topologis dasar tetap terjaga.

Dua ruang dianggap pada dasarnya sama dalam topologi jika ada homeomorfisme di antara keduanya.

Contoh: Mengubah cangkir kopi menjadi donat adalah contoh klasik homeomorfisme. Keduanya memiliki satu lubang dan bisa diubah satu sama lain melalui deformasi kontinu tanpa pemotongan atau penempelan, sehingga mempertahankan ciri topologisnya.

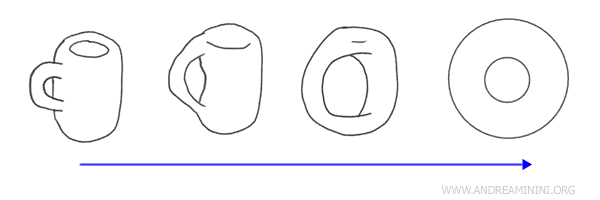
Geometri versus Topologi

Meski geometri dan topologi adalah bidang yang berbeda, keduanya saling berkaitan dengan fokus pada aspek yang berbeda dari ruang matematis.

• Geometri membahas sifat yang terkait dengan jarak, sudut, dan pengukuran, berfokus pada bangun konkret dan hubungan spasialnya. Contohnya adalah rotasi sebuah bangun, transformasi geometris yang mempertahankan jarak.
  

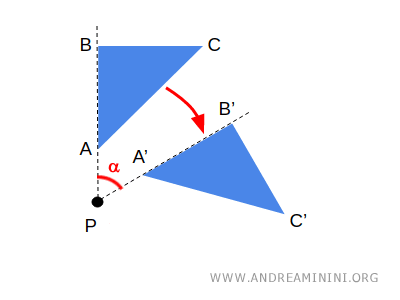
  Geometri Euclidean adalah bentuk yang paling dikenal, tetapi geometri non-Euclidean mempelajari implikasi dari melonggarkan atau meniadakan postulat kelima Euclid (postulat paralel).

• Topologi berfokus pada sifat yang tetap ada meski ruang mengalami transformasi kontinu seperti peregangan atau pemampatan, tanpa sobek atau ditempel. Bidang ini memperhatikan aspek kualitatif seperti kontinuitas, keterhubungan, dan fleksibilitas bentuk. Misalnya, mengubah kubus menjadi bola mempertahankan keterhubungan antar titik dan kontinuitas keseluruhan, yang merupakan ciri khas transformasi topologis.
  

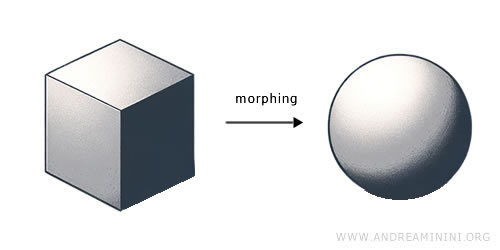
  Contoh: Sebuah kubus dari tanah liat dapat dipadatkan menjadi bola tanpa menambah atau mengurangi materi, sambil mempertahankan kontinuitas dan keterhubungan. Ini menunjukkan homeomorfisme, salah satu transformasi dasar dalam topologi.
  

Meski berbeda, topologi dan geometri memiliki keterkaitan erat, dengan topologi sering dianggap sebagai generalisasi dari geometri.

Topologi memperluas ruang kajian ke sifat-sifat abstrak ruang, berbeda dengan fokus geometri yang lebih kaku pada pengukuran.

Cabang-Cabang Topologi

Penerapan topologi meluas ke berbagai bidang matematika dan sains, dengan setiap cabang menyoroti aspek unik dari ruang topologi.

• Topologi dalam Geometri: Berfokus pada sifat yang tetap ada melalui transformasi seperti peregangan, pemampatan, dan pelipatan tanpa sobek atau ditempel. Cabang ini, dikenal sebagai topologi geometris, meneliti sifat seperti kontinuitas, keterhubungan, kekompakan, dan batas tanpa memperhitungkan jarak.
• Topologi Umum (atau Topologi Himpunan-Titik): Cabang ini mempelajari ruang topologi secara luas dan abstrak, menitikberatkan pada sifat seperti himpunan terbuka dan tertutup, kontinuitas, kekompakan, keterhubungan, serta ruang metrik dan ruang fungsi.
• Topologi Aljabar: Menggunakan alat-alat aljabar untuk mempelajari ruang topologi, dengan menghubungkan struktur aljabar pada ruang tersebut untuk lebih memahami sifat-sifatnya.
• Topologi Diferensial: Menggunakan kalkulus diferensial untuk meneliti sifat dan struktur ruang topologi, khususnya yang secara lokal mirip ruang Euclidean, sehingga memungkinkan definisi konsep seperti keterhinggapan dan keterdiferensialan.
• Topologi Terapan: Mengacu pada penggunaan metode topologi dalam aplikasi praktis di luar matematika murni, seperti analisis data, ilmu jaringan, teknik, dan biologi komputasional.

Setiap cabang topologi memiliki fokus, metode, dan penerapannya sendiri, mencerminkan fleksibilitas serta luasnya kegunaan konsep topologi.