Irisan Interior Himpunan
Jika kita mengambil interior dua himpunan \(A\) dan \(B\), lalu mengiriskannya, hasilnya selalu sama dengan interior dari irisan keduanya $ \text{Int}(A \cap B) $. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
Hasil ini menunjukkan hubungan yang sangat rapi dalam topologi. Interior \(A\) berisi semua titik yang benar-benar berada di dalam \(A\), demikian juga interior \(B\). Ketika kita mencari titik yang berada di dalam keduanya sekaligus, ternyata itulah tepatnya interior dari irisan \(A \cap B\).
Untuk memahaminya lebih mudah, ingat dua konsep penting berikut:
- Interior himpunan (\(\text{Int}(A)\)): kumpulan titik yang memiliki lingkungan terbuka yang sepenuhnya berada di dalam \(A\). Titik-titik ini tidak menyentuh batas himpunan.
- Irisan (\(\cap\)): himpunan titik yang muncul sekaligus dalam \(A\) dan dalam \(B\).
Dengan dua konsep ini, hubungan di atas menjadi lebih jelas. Irisan interior bukan hanya mirip dengan interior irisan, tetapi benar-benar identik.
Contoh Visual
Bayangkan dua lingkaran \(A\) dan \(B\) yang saling bertumpang tindih. Setiap lingkaran memiliki interiornya sendiri, yaitu seluruh area di dalam lingkaran tanpa tepinya.
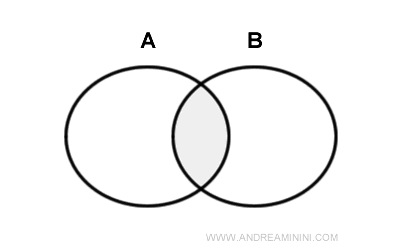
Ketika kita mengiriskan interior \(A\) dan interior \(B\), wilayah yang tersisa adalah tepat bagian dalam dari daerah yang mereka tumpangi bersama. Tidak lebih dan tidak kurang.
Pembuktian Singkat
Pembuktian teorema ini cukup elegan dan terdiri dari dua arah inklusi.
1] Inklusi Pertama (\(\subseteq\))
Jika sebuah titik berada di interior \(A\) dan interior \(B\), maka ada dua lingkungan terbuka di sekeliling titik tersebut. Keduanya sepenuhnya berada di dalam \(A\) dan \(B\). Jika kita mengambil irisan kedua lingkungan ini, hasilnya tetap sebuah lingkungan terbuka yang berada di dalam \(A \cap B\). Artinya, titik itu otomatis interior dari \(A \cap B\).
Misalkan \(x \in \text{Int}(A) \cap \text{Int}(B)\). Maka ada lingkungan terbuka \(U\) dan \(V\) sehingga \(U \subseteq A\) dan \(V \subseteq B\).
Ambil \(W = U \cap V\). Karena keduanya terbuka, \(W\) juga terbuka dan memuat \(x\).
Selain itu, \(W \subseteq A \cap B\). Maka \(x \in \text{Int}(A \cap B)\).
Jadi, \(\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)\).
2] Inklusi Kedua (\(\supseteq\))
Jika titik berada di interior irisan \(A \cap B\), maka ada lingkungan terbuka yang seluruhnya berada di dalam irisan tersebut. Lingkungan ini tentu saja juga berada di dalam \(A\) dan di dalam \(B\). Jadi titik tersebut interior dari keduanya.
Misalkan \(x \in \text{Int}(A \cap B)\). Maka ada lingkungan terbuka \(W\) sehingga \(W \subseteq A \cap B\).
Karena itu, \(W \subseteq A\) dan \(W \subseteq B\).
Maka \(x \in \text{Int}(A)\) dan \(x \in \text{Int}(B)\).
Sehingga \(\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)\).
Jika kedua arah inklusi sudah terbukti, maka kedua himpunan tersebut pasti sama:
\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]
Ini adalah salah satu contoh bagaimana konsep dasar dalam topologi dapat menghasilkan hubungan yang bersih, simetris, dan mudah diingat.