Mengenal Topologi Himpunan Terbuka

Secara sederhana, topologi adalah cara untuk menentukan mana saja himpunan bagian dari X yang disebut "terbuka", dengan syarat bahwa kumpulan ini tertutup terhadap operasi gabungan dan irisan.

Sebuah koleksi himpunan berarti himpunan yang elemen-elemennya juga berupa himpunan. Jadi, di sini kita berbicara tentang "himpunan dari himpunan".

Jika kita memiliki himpunan X dan topologi T yang sesuai, maka keduanya membentuk ruang topologi, biasanya ditulis sebagai pasangan (X,T).

Catatan: sering kali orang hanya mengatakan "X adalah ruang topologi", tetapi sebenarnya ruang topologi terdiri dari dua bagian: himpunan X itu sendiri dan topologi T, yaitu kumpulan himpunan bagian yang dianggap terbuka.

Mengapa Himpunan Kosong Selalu Terbuka?

Himpunan kosong didefinisikan sebagai himpunan terbuka di setiap ruang topologi. Ini bukan kebetulan, melainkan kesepakatan penting agar sifat-sifat dasar topologi tetap konsisten dan lengkap. Tanpa aturan ini, banyak hasil dalam topologi tidak akan berlaku dengan baik.

Contoh Sederhana

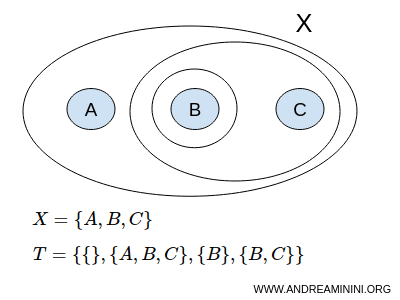
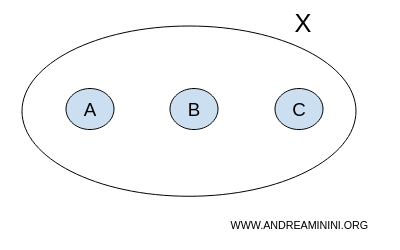
Bayangkan kita memiliki himpunan X dengan tiga elemen A, B, dan C:

$$ X = \{ A,B,C \} $$

Salah satu kemungkinan topologi pada X adalah koleksi berikut:

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

Di sini { } melambangkan himpunan kosong, sedangkan {A,B,C} adalah himpunan penuh X. Keduanya, berdasarkan definisi, termasuk himpunan terbuka.

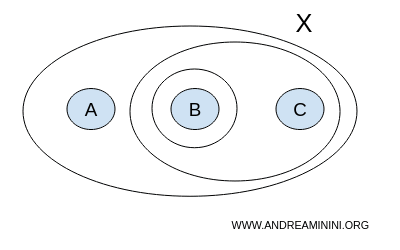
Untuk memastikan bahwa T benar-benar sebuah topologi, kita harus memeriksa apakah ia tertutup terhadap operasi gabungan dan irisan:

• Gabungan dari dua himpunan terbuka harus tetap terbuka.
• Irisan dari dua himpunan terbuka juga harus terbuka.

Contohnya:

$$ \{ B \} \cup \{ B, C \} = \{ B, C \} \subseteq T$$

$$ \{ B \} \cap \{ B, C \} = \{ B \} \subseteq T$$

Karena semua gabungan dan irisan menghasilkan himpunan yang masih ada di dalam T, maka T benar-benar merupakan topologi dari X.

Contoh Lain: Ketika Koleksi Tidak Menjadi Topologi

Sekarang kita ubah sedikit contoh sebelumnya. Himpunan X tetap sama:

$$ X = \{ A,B,C \} $$

Kita tambahkan himpunan bagian {A} ke dalam koleksi T:

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

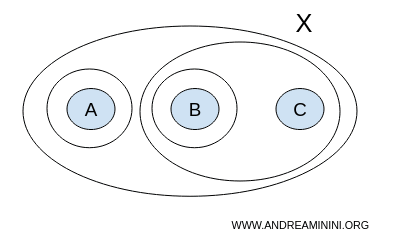
Sekilas terlihat mirip, tetapi koleksi ini bukan topologi. Mengapa? Karena gabungan dari {A} dan {B} menghasilkan {A,B}, dan himpunan {A,B} tidak termasuk dalam koleksi T.

$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T  $$

Jadi, meskipun {A} dan {B} masing-masing dianggap "terbuka", gabungan keduanya tidak lagi terbuka dalam koleksi ini. Hal ini melanggar salah satu syarat utama topologi.

Kesimpulannya, koleksi T ini tidak dapat disebut topologi pada himpunan X.

Contoh ini menunjukkan bagaimana definisi topologi membantu kita memahami struktur himpunan dan konsep "keterbukaan" dengan cara yang lebih sistematis dan konsisten.