集合的内点集

在拓扑空间 \( X \) 中，设 \( A \subseteq X \)。由 \( A \) 的所有内点组成的集合称为 \( A \) 的内点集，也常简称为 \( A \) 的内部。等价地，内点集可以看作是所有包含于 \( A \) 内的开子集的并集，通常记为 \( \text{Int}(A) \) 或 \( A^\circ \)。

直观地说，集合的内点集描述了那些“完全位于集合内部”的点所构成的最大开集。

在所有包含于 \( A \) 的开子集中，不存在比 \( A \) 的内点集更大的开集。

说明：内点集的基本性质直接来自其定义。由于它是若干开集的并，因此内点集本身必然仍是开集。

从点的角度来看，若 \( x \in A \)，并且存在一个开邻域 \( U \)，使得 \( x \in U \subseteq A \)，那么点 \( x \) 就称为 \( A \) 的内点。所有内点汇集在一起，便得到 \( A \) 的内点集。

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ 在 } X \text{ 中是开集} \} $$

因此，点 \( x \) 属于 \( \text{Int}(A) \)，当且仅当存在某个开集 \( U \)，满足 \( x \in U \) 且 \( U \subseteq A \)。

需要特别注意的是，集合 \( A \) 的内点集依赖于其所处的拓扑空间 \( X \)，而不是集合 \( A \) 本身的性质。在不同的拓扑结构下，同一个集合的内点集可能并不相同。

一个具体例子

考虑实数集 \( \mathbb{R} \) 中的集合 \( A = [0,1] \)，并采用标准拓扑。

该区间包含从 0 到 1 的所有实数。

在标准拓扑下，集合 \( A \) 的内点集是开区间 \( (0,1) \)。

$$ \text{Int}(A) = (0,1) $$

这是完全包含在 \( [0,1] \) 内的最大开区间。端点 0 和 1 位于边界上，不属于任何完全包含于 \( A \) 的开区间，因此不是内点。

例 2

再看集合 \( A = [0,1) \)，仍位于 \( \mathbb{R} \) 中，并采用标准拓扑。

这是一个左闭右开的区间，包含 0 而不包含 1。

在这种情况下，集合 \( A \) 的内点集依然是 \( (0,1) \)：

\[ \text{Int}(A) = (0,1) \]

原因在于，内点集只关心那些能够被开区间完全包住的点，而端点 0 无法满足这一条件。

说明：在 \( \mathbb{R} \) 的标准拓扑中，开区间是最基本的开集。对于 \( [0,1) \)，唯一的极大开子集是 \( (0,1) \)，它恰好刻画了所有内点。

例 3

下面仍然考虑集合 \( A = [0,1) \)，但这一次在 \( X \) 上赋予离散拓扑。

在离散拓扑空间中，\( X \) 的任意子集都是开集。

这意味着，集合 \( A \) 中的每一个点，都可以被某个完全包含在 \( A \) 内的开邻域所包围。

在 \( \mathbb{R} \) 上采用离散拓扑时，所有子集都是开集。这不仅包括各种区间，还包括任意有限或无限的点集。因此，像 \( (0,0.5) \)、\( (0.25,0.75) \)、\( (0,1) \)，以及包含于 \( A=[0,1) \) 的闭区间 \( [0,0.25] \)，连同空集和整个集合 \( [0,1) \) 本身，统统都是开集。

由于 \( A = [0,1) \) 本身就是开集，它的内点集自然等于自身。

$$ \text{Int}(A) = A = [0,1) $$

在离散拓扑中，任何集合的内点集都与该集合完全一致。

说明：这个例子清楚地展示了拓扑结构对内点和内点集概念的影响。改变拓扑，集合的“内部”性质也会随之发生变化。

例 4

设拓扑空间 \( X = \{a,b,c\} \)，并在其上采用离散拓扑。

在这种拓扑下，\( X \) 的每一个子集都是开集：

• \( \emptyset \) 和 \( \{a,b,c\} \) 是开集。
• 单点集 \( \{a\} \)、\( \{b\} \)、\( \{c\} \) 也是开集。
• 由两个点组成的集合，如 \( \{a,b\} \)、\( \{a,c\} \)、\( \{b,c\} \)，同样是开集。

现在考虑集合 \( A = \{b,c\} \)。

根据内点集的定义，\( \text{Int}(A) \) 是所有包含于 \( A \) 内的开子集的并。

这些开子集正是 \( \{b\} \)、\( \{c\} \) 和 \( \{b,c\} \)。

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b,c\} = \{b,c\} \]

因此，在该拓扑下，集合 \( A \) 的内点集与 \( A \) 本身完全相同。

说明：这一结论对离散拓扑空间中的任意子集 \( S \subseteq X \) 都成立。由于所有子集都是开集，其内点集必然等于自身，即 \( \text{Int}(S) = S \)。

集合的内点定理

在拓扑空间 \( X \) 中，设 \( S \subseteq X \)，\( y \in X \)。当且仅当存在一个开集 \( U \)，使得 \( y \in U \subseteq S \) 时，点 \( y \) 属于集合 \( S \) 的内点集，记为 \( \text{Int}(S) \)。用符号表示为：$$ y \in \text{Int}(S) \iff \exists \ U \text{ 为开集，使得 } y \in U \subseteq S $$

直观来看，只要点 \( y \) 能够被某个完全包含在集合 \( S \) 内的开集所“包住”，那么它就位于 \( S \) 的内部。

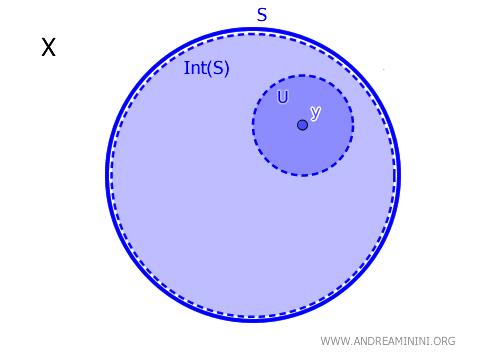
该定理为判断一个点是否属于集合的内部提供了一个清晰而严格的充要条件，是理解内点概念的核心结果。

证明

• 必要性：若 \( y \in \operatorname{Int}(S) \)，按照内点集的定义，必然存在一个开集 \( U \subseteq X \)，使得 \( y \in U \) 且 \( U \subseteq S \)。因此，定理中的必要条件成立。
• 充分性：若存在开集 \( U \)，满足 \( y \in U \subseteq S \)，由于内点集是所有包含于 \( S \) 的开集的并，必有 \( U \subseteq \operatorname{Int}(S) \)，从而 \( y \in \operatorname{Int}(S) \)。

说明：内点定理在拓扑学中处于基础地位。它将“点属于集合内部”这一直观想法精确地转化为开集的存在性，是研究连续性和其他拓扑性质的重要起点。

例

考虑实数集 \( \mathbb{R} \) 中的集合 \( A = [1,3] \)，并赋予标准拓扑。

$$ A = [1,3] $$

该集合包含从 1 到 3 的所有实数。

下面利用内点定理来确定集合 \( A \) 的内点集。

根据定义，需要找到一个开集 \( U \)，使得 \( U \subseteq A \)，并且 \( U \) 中的每一个点都位于 \( A \) 的内部。

1. 选取开集 \( U \)
   取 \( U = (1,3) \)，这是一个不包含端点的开区间，因此在 \( \mathbb{R} \) 的标准拓扑下是开集。
2. 验证 \( U \subseteq A \)
   区间 \( (1,3) \) 中的任意点都属于闭区间 \( [1,3] \)，而端点 1 和 3 并不包含在 \( U \) 中，这与开区间的定义一致。

由此可见，\( U \) 是一个完全包含在 \( A \) 内的开集，这说明 \( (1,3) \) 中的所有点都是 \( A \) 的内点。因此：

$$ \operatorname{Int}(A) = (1,3) $$

说明：该例表明，集合 \( A \) 的内点集是开区间 \( (1,3) \)。边界点 1 与 3 不属于内点集，因为不存在一个既包含这些点又完全包含于 \( A \) 的开区间。

内点集的基本性质

下面总结拓扑空间中与内点集相关的一些常见性质。这些结论有助于理解内点运算与并集、交集以及闭包等操作之间的关系。

• 内点集与并集
  两个集合内点集的并，始终包含于它们并集的内点集中，但一般不相等。$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
• 内点集与交集
  两个集合内点集的交，恰好等于这两个集合交集的内点集。$$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
• 补集、内点与闭包
  集合 \( A \) 的补集的内点等于 \( A \) 的闭包的补集。$$ \text{Int}(X - A) = X - \text{Cl}(A) $$
• 补集的闭包与内点集的补集
  集合 \( A \) 的补集的闭包等于 \( A \) 的内点集的补集。$$ \text{Cl}(X - A) = X - \text{Int}(A) $$

补充说明

以下结论在实际学习和应用中尤为常用。

• 若 \( U \) 是 \( X \) 中的开集且 \( U \subseteq A \)，则 \( U \subseteq \text{Int}(A) \)
  由于 \( \text{Int}(A) \) 是包含于 \( A \) 的最大开集，任何位于 \( A \) 内的开集都会自动包含在 \( \text{Int}(A) \) 中。
• 若 \( A \subseteq B \)，则 \( \text{Int}(A) \subseteq \text{Int}(B) \)
  这表明取内点集这一运算保持集合之间的包含关系。
• 集合 \( A \) 是开集，当且仅当 \( A = \text{Int}(A) \)
  该结论为判断一个集合是否为开集提供了一个直接而有效的标准。
• 利用 R 语言计算集合的内点集
  在具体模型或计算场景中，可以借助 R 语言对集合的内点集进行分析与计算。

依此类推。