开集拓扑：从概念到直观理解

换句话说，拓扑 T 是由一组被视为开集的子集构成的结构，并在并运算和交运算下保持封闭。这类集合族也称为集合族，即元素本身是集合的集合。

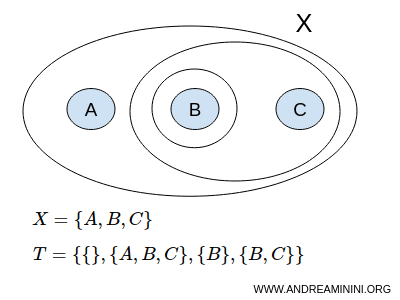
当集合 X 与拓扑 T 搭配在一起时，我们称它们构成了一个拓扑空间，记作 (X,T)。

说明：为了表述简洁，我们常直接说"X 是一个拓扑空间"，但实际上拓扑空间由两部分组成，即集合 X 和拓扑 T。

为什么空集一定是开集

在任何拓扑中，空集被定义为开集。这并非为了形式上的方便，而是为了确保拓扑公理自洽并可正确推导各种性质。如果空集不被视为开集，许多拓扑结论将无法成立。

从一个例子入手理解拓扑

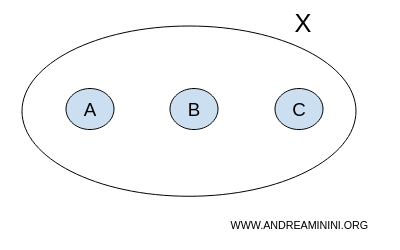
设集合 X 含有三个元素：

$$ X = \{ A,B,C \} $$

一种可能的拓扑 T 是：

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \} \} $$

其中空集 Ø 与全集 {A,B,C} 是拓扑所要求的基本开集。

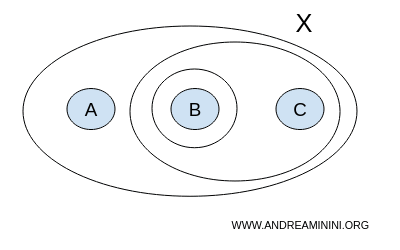
在这个例子中，T 之所以是拓扑，是因为它满足开集运算封闭性：

它对并运算封闭：

$$ \{ B \} \cup \{ B, C \} = \{ B, C \} \in T$$

$$ \{ B \} \cup \{ \} = \{ B \} \in T $$

它对交运算也封闭：

$$ \{ B \} \cap \{ B, C \} = \{ B \} \in T$$

$$ \{ B \} \cap \{ \} = \{ \} \in T $$

因此，T 可以作为集合 X 的一个拓扑。

反例：看似合理但不是拓扑

再来看一个类似的集合族：

$$ X = \{ A,B,C \} $$

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$

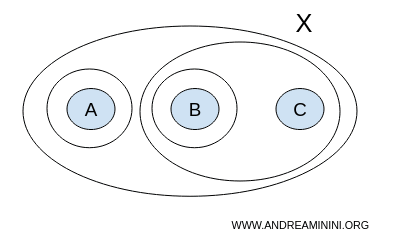
这个 T 虽然看起来与前例非常接近，但它不是拓扑。原因在于：

$$ \{ A \} \cup \{ B \} = \{ A,B \} \notin T $$

既然 {A} 和 {B} 被视为开集，它们的并也必须是开集。但 {A,B} 不属于 T，这违反了拓扑对并运算封闭的要求。因此它不能成为拓扑。

总结

拓扑是"开集结构"，它定义了集合中哪些子集可以被视为开集，并要求在基本集合运算下保持封闭。通过正反两个例子，我们可以看到拓扑的本质并不在于给出尽可能多的开集，而是在于保持结构上的一致性。

掌握这个核心思想，有助于进一步理解连通性、连续性以及后续更深入的拓扑概念。