开集
如果在集合 A 中,对任意一点 x(x∈A)都能找到一个完全包含在 A 内的邻域,那么 A 就称为一个开集。
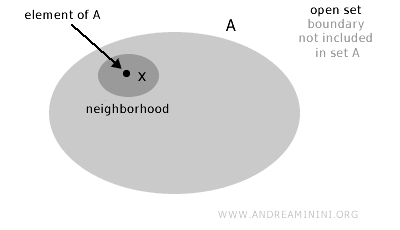
通俗来说,一个集合如果不包含它的"边界点",就可以视为开集。
严格地讲,在拓扑空间 X 中,集合 A 是开集,当且仅当对 A 中每个点 x,都存在一个邻域完全落在 A 内。
注意:这意味着对集合中任意一点,都能找到一块完全位于集合内部的小区域,不会与集合外部发生接触。
直观例子
在数轴上,开区间是最常见也最易理解的开集例子。
什么是开区间? 在 \( \mathbb{R} \) 上,开区间指所有满足 \( a < x < b \) 的实数 x,其中 a 和 b 为实数且 a < b。
记作 (a,b),圆括号表示端点 a 和 b 不属于该集合。
例如,区间 (3,10) 是实数轴上的一个开集。
此时,集合 A 含有所有大于 3 且小于 10 的实数,不包括端点。
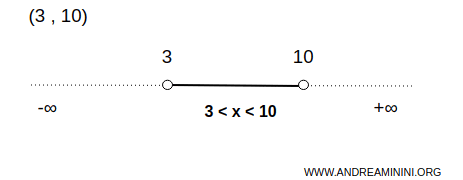
在该区间内,每一个点 x 都可以找到一个更小的开区间,使其完全包含在 (3,10) 之内。
例如,对 x=3.1,可以选择开区间 (3.09,3.11),它完全位于 (3,10) 内。
同理,区间内任意一点都可以这样处理,因为在任何两个实数之间都存在无穷多个实数。
注意:即使取非常接近边界的点,例如 3.001,我们依然能构造它的邻域(如 3.001±0.00000001),并且这个邻域依旧完全落在开区间 (3,10) 内。
这是最基本的一维开集示例。
更多例子
开集的概念可以自然推广到二维平面。
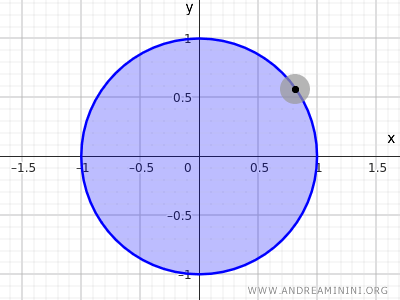
例如,以原点 (0,0) 为圆心、半径 r=1 的圆内部所有点:
$$ x^2+y^2<1 $$
该不等式描述的是所有距离圆心小于 1 的点,只包含圆内部,不包含圆周。
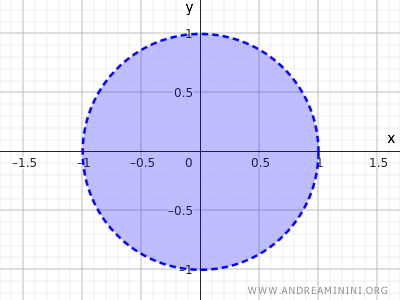
这就是二维空间中的一个开集。
那么闭集是什么?
如果我们把圆周上的点也加入集合,就得到一个闭集:
$$ x^2+y^2 \le 1 $$
此时就不再满足"每个点都拥有完全落在集合内部的邻域"这一性质。
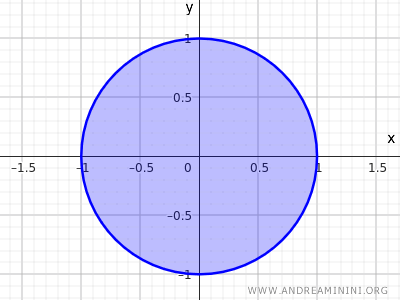
特别是圆周上的点无法拥有这样的邻域。
注意:在欧氏空间 R2 中,圆方程 \( x^2+y^2=1 \) 所描述的点集既不是开集也不是闭集,因为它只包含圆周本身;而 \( x^2+y^2<1 \) 是开集;如果改为 \( x^2+y^2\le 1 \),则该集合是闭集。
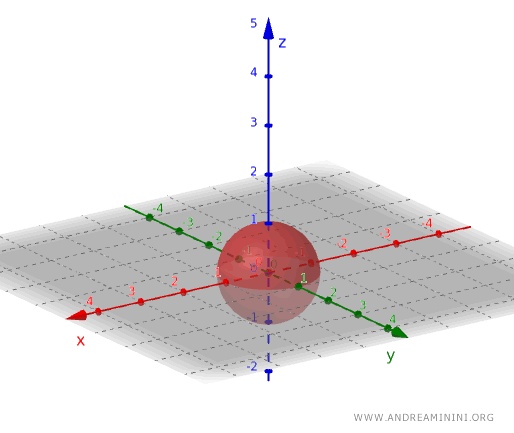
同样地,在三维空间中,球体内部(不含球面)构成一个开集。
拓扑的选择
开区间之所以常被使用,是因为它直观易懂,有助于形成对开集的初步理解。
然而,开集的概念远比开区间更一般,也更抽象。
在掌握直观例子之后,我们必须进一步提升对其本质的认识。
一个集合是否为"开集",取决于赋予空间的拓扑结构。
关键思想是:开集的定义依赖于拓扑,而不同拓扑会给出截然不同的开集。
在某些拓扑中,看起来"闭"的集合,在另一种拓扑下可能是"开"的。
换言之,"开"的含义来源于拓扑本身。
什么是拓扑? 拓扑是一组被规定为"开集"的集合族,它必须满足一些基本规则,例如任意多个开集的并仍为开集,有限多个开集的交仍为开集。
因此,我们不应把视野局限在开区间或开圆盘这些最直观的例子上。
在拓扑学中,有些集合乍看之下不像开集,却可能在某种拓扑下被视为开集。
一个更抽象但重要的例子
考虑仅包含两个元素的集合 \( \{a, b\} \)。
在这个集合上,可以定义至少两种拓扑:平凡拓扑和离散拓扑。
- 平凡拓扑
在平凡拓扑中,唯一的开集是空集 \( \emptyset \) 和全集 \( \{a, b\} \)。这是最简单的拓扑结构。 - 离散拓扑
在离散拓扑中,每个子集都是开集。因此 \( \{a\} \)、\( \{b\} \)、\( \{a,b\} \) 和 \( \emptyset \) 全部是开集。
现在对集合 \( \{a\} \) 考察:
- 在平凡拓扑中,{a} 不是开集
因为唯一的非空开集只有 \( \{a,b\} \)。 - 在离散拓扑中,{a} 是开集
因为该拓扑中所有子集都被定义为开集。
因此,集合 \( \{a\} \) 是否为开集,取决于所选拓扑。
这个例子清楚展示了开集概念与拓扑选择之间的紧密关系。
开集定理
定理一
设拓扑空间为 (X,T),其中 X 为空间,T 为其拓扑。若子集 S ⊂ X 满足:对任意一点 s ∈ S,都存在一个邻域 U,使得 U 完全包含在 S 内,即 U ⊂ S,则 S 为开集。
根据定义,S 之所以是开集,是因为它属于拓扑空间 (X,T) 的开集族。
换句话说,对于 S 内的任意一点 s ∈ S,总能找到一个属于 S 的邻域。
因此,每个元素 s ∈ S 都存在一个开邻域 Us,它完全包含在 S 中。
$$ x \in U_s \subset S \subset X $$
由此可知,一个开集可以视为其所有开邻域的并。
因此,只要观察到 S 中每个点 s ∈ S 都有邻域 Us 满足 Us ⊂ S,便可断定 S 是开集,因为 S 是开集的并。
也就是说,一个集合是开集,当且仅当对于集合中每一点,都存在一个完全落在该集合之内的邻域。
例子:想象一张桌子,上面散落着许多玻璃弹珠,每颗弹珠代表集合中的一个点。若一个集合是"开集",意思是无论选中哪颗弹珠,它周围总能有足够的空间自由移动,而不会触碰桌子的边缘。若对桌上的每一颗弹珠,我们都能画出一个完全位于桌面范围内的小圆,那么这些弹珠构成的集合就对应一个开集。本质上,开集意味着:无论我们选中哪一点,都能找到一块仍属于该集合的"活动空间"。

定理二
设 \( X \) 是一个集合,\( B \) 是拓扑的一个拓扑基。若子集 \( A \subset X \) 满足:对任意一点 \( x \in A \),都存在一个基元素 \( B_x \in B \),使得 \( x \in B_x \) 且 \( B_x \subseteq A \),则 \( A \) 是由 \( B \) 所生成拓扑中的开集;反之亦然。
该定理刻画了由拓扑基生成的拓扑的核心特征。
换言之,开集 \( A \) 中的每一点 \( x \) 都必须拥有一个来自拓扑基的开邻域 \( B_x \),并且该邻域完全包含在 \( A \) 内。
因此,\( A \) 在由 \( B \) 生成的拓扑中是开集。
证明:若 A 是由拓扑基 B 在 X 上生成的开集,则根据定义,A 是若干基元素的并。因此对任意 \( x \in A \),存在至少一个基元素 \( B_x \),满足 \( x \in B_x \subseteq A \)。反之,若对任意 \( x \in A \) 都可找到基元素 \( B_x \),使得 \( x \in B_x \subseteq A \),则 A 是基生成拓扑中的开集。
例 1
设 \( X = \{1, 2, 3, 4, 5\} \),其拓扑基为 \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \)。判断集合 \( A = \{1, 2, 3\} \) 是否为开集。
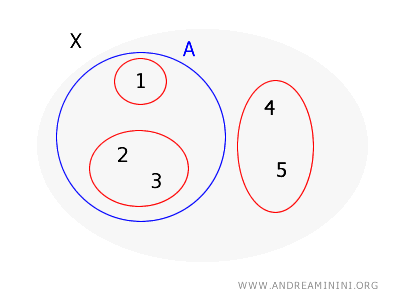
对 A 中的每个点检查:
- 点 \( 1 \):对应基元素 \( \{1\} \),完全包含于 \( A \)。
- 点 \( 2 \):对应基元素 \( \{2, 3\} \),完全包含于 \( A \)。
- 点 \( 3 \):同样属于 \( \{2, 3\} \),完全包含于 \( A \)。
因此,\( A \) 是开集,因为它满足定理要求。
例 2
继续使用同一集合 \( X = \{1, 2, 3, 4, 5\} \) 及拓扑基 \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \)。
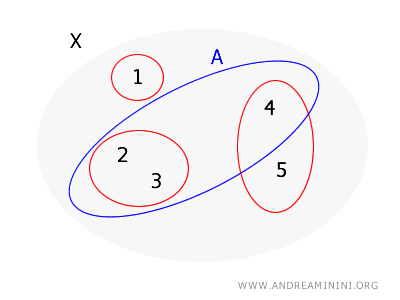
判断集合 \( A = \{2, 3, 4\} \) 是否为开集:
- 点 \( 2 \):对应基元素 \( \{2, 3\} \),包含于 \( A \)。
- 点 \( 3 \):仍由 \( \{2, 3\} \) 覆盖并包含于 \( A \)。
- 点 \( 4 \):唯一的基元素是 \( \{4, 5\} \),但其中的 5 不属于 \( A \),因此不存在完全包含于 \( A \) 的基元素覆盖点 4。
由定理可知,\( A \) 不是开集,因为并非所有点都能找到完全包含于 \( A \) 的基元素。
附注
关于开集的一些补充:
- A 是开集当且仅当 A = Int(A)
在拓扑空间 \( X \) 中,集合 \( A \) 是开集,当且仅当它等于其内部。内部 Int(A) 定义为所有包含于 \( A \) 的开集的并。$$ A = \text{Int}(A) $$
未尽部分可继续拓展。