拓扑学中的单连通空间

在拓扑学中，如果一个空间内的任意封闭路径都能在不离开该空间的情况下连续缩成一个点，那么这个空间就被称为单连通空间。

换句话说，若空间中的任何环路都可以在空间内部逐渐"收紧"成一个点，而不需要跨出空间边界，那么这个空间就是单连通的。

这表示该空间是一个没有内部空洞的整体结构 - - 一个完整且连贯的"整体"空间。

注意：单连通空间一定是连通空间，但连通空间不一定是单连通的。这是两种不同层次的连通性。

直观示例

最典型的例子是球面。球面上的任何封闭曲线都可以在不离开球面的情况下连续地收缩成一个点，因此球面是单连通空间。

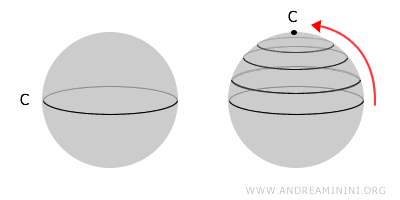
与此相对的是圆环（或称"甜甜圈"形空间）。由于它的中心存在一个空洞，某些环路会被空洞"卡住"，无法收缩为一点，所以它不是单连通的。

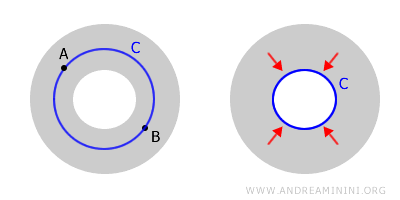
这进一步说明，空间的连通性并不一定意味着单连通。圆环依然是连通的，因为空间中任意两点都能通过一条完全位于内部的路径相连。

但它不是单连通的，因为存在无法收缩到一点的环路。

这种"连通但非单连通"的空间称为多连通空间。典型例子包括环形区域和环面。

因此，单连通性是一种比路径连通性更严格的条件，它揭示了空间结构中"空洞"的存在与否。

理解这一点，是深入学习拓扑学的关键一步。