拓扑基

拓扑基指拓扑空间 T 中一组能够“生成”所有开集的集合 B。换言之，T 中的任意开集都可以写成 B 中若干基开集的并。

设 X 是一个集合，T 是 X 上的一个拓扑，由 X 的若干子集组成。拓扑 T 的一组基是一个集合 B，其元素称为基开集。B 必须满足以下两个基本条件：

• X 中的每个点 x 都至少属于 B 中的某个基开集。
• 若点 x 同时属于两个基开集 B₁ 和 B₂ 的非空交集，则在该交集中应当还能找到一个包含 x 的基开集 B₃。也就是说，基开集在交点附近具有足够的“局部细化性”。
  

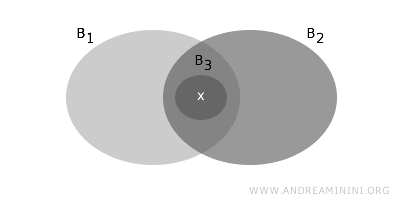
满足上述条件后，B 便构成拓扑 T 的一组基。

为什么需要拓扑基？

拓扑基提供了一种更简洁的方式来描述拓扑。与其直接给出所有开集，不如从一组基开集出发，通过取并即可恢复整个拓扑结构。这在理论研究与实际构造中都非常方便。

Note. 基开集交集条件确保拓扑满足核心公理，包括两开集的交集仍为开集这一基本性质。

例 1：有限集合上的拓扑基

设

$$ X=\{a,b,c\} $$

拓扑为：

$$ T=\{ \emptyset, \{a\}, \{b,c\}, \{a,b,c\} \} $$

这表示 X 上全部的开集。

一种可能的拓扑基是：

$$ B=\{ \{a\}, \{b,c\} \} $$

它确实是一组基，因为 X 中的每一个点都出现在 B 的某个集合中，且两个基元素之间不存在需要处理的交集情况。

注意，T 中的每个开集都能用 B 中的集合取并得到：

$$ \{a\} \in B $$

$$ \{b,c\} \in B $$

$$ \{a,b,c\} = \{a\} \cup \{b,c\} $$

Note. 在集合论中，空集 Ø 始终是任何集合的非真子集，因此自然包含在拓扑中，也属于 B。$$ \emptyset \in B $$ 另外，空集在任何拓扑中都被定义为开集。

这个例子展示了有限环境下开集的构造方式。

在无限或更复杂的空间中，拓扑基的选择可能更讲究，但核心思路始终一致：基开集提供构成整个拓扑的基本“构件”。

另一种可行的拓扑基

在同一集合 X={a,b,c} 上，也可以选择另一组基：

$$ B=\{ \{a\}, \{b\}, \{c\} \} $$

这是一组由单点集组成的基。

可以验证，此基仍能生成拓扑 T={Ø,X,{a},{b,c}}：

• 空集 Ø 作为开集按定义存在。
• 集合 {a} 已在 B 中。$$ \{a\} \in B $$
• 集合 {b,c} 可由 {b} 与 {c} 的并得到。$$ \{b,c\} = \{b\} \cup \{c\} $$
• 整个集合 X 可由三个单点集的并得到。$$ \{a,b,c\} = \{a\} \cup \{b\} \cup \{c\} $$

因此，这组基同样能完整生成 T 中所有开集。

Note. 这说明同一拓扑可能有多组不同的基，每一组基都从不同角度揭示了拓扑的结构。

例 2：实数轴的标准拓扑基

实数轴 R 上最常用的拓扑基是所有开区间 (a,b)，其中 a

$$ B=\{(a,b)\subset R \mid a

这是拓扑学中的经典构造，因为任意实数点都能落在某个左开右开区间 (a,b) 中。

此外，若两个区间相交，则交集中的任意一点附近都能找到一个更小的开区间完全包含在交集中，这个区间也属于基 B。

例如，区间 (0,3) 与 (2,4) 的交集是 (2,3)。

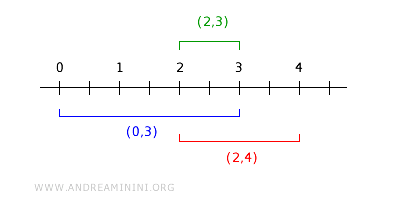
区间 (2,3) 本身就是基中的某个 B_i，并且完全位于这两个区间的交集内。$$ (0,3) \cap (2,4) = (2,3) ∈  B_i ⊂ (0,3) \cap (2,4) ⊂ B $$

可数基

可数基是指拓扑空间 \( X \) 上一族"可数的"开集 \( \mathcal{B}=\{B_1,B_2,B_3,\dots\} \)，并满足：空间中任意开集都可以表示为这些基开集的并。

若一个集合包含有限个元素，或其元素能够与自然数集合 \( \mathbb{N} \) 建立一一对应关系，则称该集合是"可数"的。

换言之，一个集合是可数的，就是说其元素可以按顺序编号为 \( B_1,B_2,B_3,\dots \)。

基与可数基之间的区别是什么？

任何拓扑基都能生成拓扑，但只有那些元素数量在集合论意义上"足够小"的基，即元素可数的基，才称为可数基。

拓扑空间具有可数基是一个非常重要的性质。例如，可数基是乌里森度量化定理（Urysohn's Metrization Theorem）的关键条件之一。此外，分析与拓扑中的许多基本结论在可数基空间中更容易处理，甚至只在可数基空间中成立。

例子

在标准拓扑下的实数集 \( \mathbb{R} \) 中，所有端点为有理数、满足 \( a < b \) 的开区间 \( (a,b) \)，构成一组可数基。

这是因为我们可以将所有此类区间依次列举，如 I₁、I₂、I₃ 等。

证明

自然数集合是可数的，因为它能依次列出：

\[ 1,\ 2,\ 3,\ 4,\ 5,\ \dots \]

如果可以对所有满足 \( a < b \) 且端点为有理数的开区间 \( (a,b) \) 进行类似的列举，那么这组区间也是可数的。

有理数虽然无限，但它们是可数的。例如，可按如下方式排列：

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

将它们记为 \( q_1,q_2,q_3,\dots \)。

然后考虑所有满足 \( q_i

如：

• \( (q_1,q_2)=(0,1) \)
• \( (q_3,q_2)=(-1,1) \)
• \( (q_4,q_5)=(\tfrac{1}{2},-\tfrac{1}{2}) \) ❌ 因为 \( a>b \) 不成立
• \( (q_5,q_1)=(-\tfrac{1}{2},0) \)
• ...

每一对满足 \( a < b \) 的有理数有序对都定义了一个开区间。

因此，这些区间可以按顺序排列，例如：

1. \( (0,1) \)
2. \( (-1,1) \)
3. \( (-\tfrac{1}{2},0) \)
4. \( (0,\tfrac{1}{2}) \)
5. \( (-1,\tfrac{1}{2}) \)
6. \( (\tfrac{1}{2},1) \)
7. \( (-\tfrac{2}{3},0) \)
8. \( (0,\tfrac{2}{3}) \)
9. \( (-1,\tfrac{2}{3}) \)
10. \( (-\tfrac{1}{2},\tfrac{1}{2}) \)
11. ...

换言之，尽管这些区间数量无限，但它们可以像自然数一样逐一定义并列举出来。这正是集合"可数"的含义。

因此，所有端点为有理数且满足 \( a < b \) 的开区间构成的集合是可数的，因为我们可以在数学意义上对其进行枚举，并确保无遗漏。

补充说明

关于拓扑基的一些进一步说明如下：

• 若在集合 X 上构造拓扑基 B，使得每个元素 x∈X 对应单点集 {x}∈B，则可从这组基生成 X 上的任意拓扑。

  单点集的任意并可以产生 X 上的任意开集，因此能够生成任意拓扑。
  
  例如，对于 X={a,b,c}，基 B={ {a}, {b}, {c} } 可生成拓扑 T={Ø,{a},{b,c},X}。
  
  同样的基 B 也可生成 X 上的其他拓扑，例如 T={Ø,{b},{a,c},X}，或平凡拓扑 T={Ø,X}，或离散拓扑 T={Ø,{a},{b},{c},{a,b},{a,c},{b,c},X} 等等。

  Note. 第一条件成立，因为 X 的每个元素都出现于 B 的单点集中。第二条件成立，是因为单点集两两不交，每个集合都只含一个点。

依此类推。