实数集上的标准拓扑

标准拓扑是实数集 R 上最常用的一种拓扑结构。在这种拓扑中，所有形如 (a, b)（其中 a < b） 的开区间，以及它们任意数量的有限或无限并集，都被定义为开集。

换句话说，一个集合 U 是开集，当且仅当对 U 中的每一个点 x，都能找到一个开区间 (a, b)，使得 x 位于其中，并且这个区间 (a, b) 完全包含在 U 内。

$$ x \in (a,b) \subseteq U $$

也就是说，开集 U 的每个元素 x 都处在某个包含于 U 的开区间内。

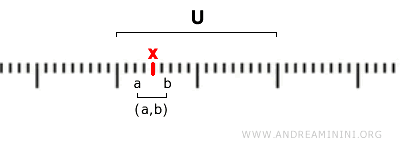
因此，在标准拓扑下，下列集合都属于开集：

• 开区间
  实数集 \( \mathbb{R} \) 的标准拓扑以所有开区间 \( (a, b) \)（a < b）为基础，这些区间及其任意并集都构成开集。
• 集合运算
  在标准拓扑中，开集对某些集合运算是封闭的。
  • 并集：任意多个开集的并集始终是开集。
  • 有限交集：有限个开集的交集依然是开集。

标准拓扑只是可以在集合 X 上定义的众多拓扑结构之一。它之所以被称为“标准”，是因为这种结构最符合我们对“邻近性”“开性”和“连续性”的直观理解，也因此被广泛应用于数学的各个领域。

在实数轴 R 上，这种拓扑尤其重要，因为它自然地反映了数轴上点与点之间的距离和连续变化关系。

提示：在 R 或其他集合上还可以定义不同的拓扑基，从而得到与标准拓扑不同的结构。这些变体通常用于研究特定性质，或在不同数学场景中探索新的思路。

实例讲解

在实数集 R 上，标准拓扑的基由所有满足 a < b 的开区间 (a, b) 构成。

$$ B = \{ (a,b) \subset; R \ | \ a \lt b \} $$

这种拓扑有一个重要特征：对任意开集 U 中的点 x，总能找到一个足够小的区间 (x-ε, x+ε)，它完全包含在 U 内。这就是标准拓扑中开集的本质特征。

$$ \forall \ x \ \in U \ \exists \ \epsilon>0 \ | \ x \in (x-\epsilon, x+\epsilon) \subseteq U $$

标准拓扑之所以“标准”，是因为它在实数轴上提供了最自然、最常用的空间结构。

示例 2

考虑区间 (0,1)，即不包含端点 0 和 1 的实数区间，并在其上应用标准拓扑。

问题是，这个区间是否本身构成一个拓扑空间？

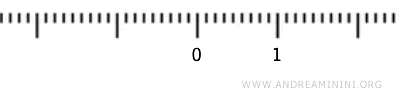
在这种情况下，当 \( U \subset (0, 1) \) 时，如果对每个 \( x \in U \)，都能找到一个实数集 \( \mathbb{R} \) 中的开区间 \( (a, b) \)，使得 \( x \in (a, b) \) 且 \( (a, b) \cap (0, 1) \subseteq U \)，那么 U 就是 (0,1) 中的开集。

事实上，区间 (0,1) 可以看作是实数集标准拓扑下若干开集的交集。

因此，区间 \( (0, 1) \) 在 \( \mathbb{R} \) 的标准拓扑诱导下，构成一个独立的拓扑空间。

例如，\( (0.1, 0.5) \)、\( (0.2, 0.9) \)，以及它们的并集 \( (0.1, 0.5) \cup (0.6, 0.8) \)，在诱导拓扑下都属于 \( (0, 1) \) 的开集。换句话说，\( (0, 1) \) 中的开集，就是实数集中的开集在该区间内的限制。

由于 \( (0, 1) \) 是 \( \mathbb{R} \) 的子空间，它在诱导拓扑下仍然满足拓扑空间的基本性质。

示例 3

再看一个例子：有限集合 X = {1, 2, 3}。

能否在实数集 \( \mathbb{R} \) 的标准拓扑下，把它看作一个拓扑空间？

答案是否定的。因为标准拓扑是以开区间为基础定义的，而对于有限集合 X，单个元素无法形成开区间。

例如，把 X 中的元素 {2} 看作实数 2。它虽然位于区间 (2-ε, 2+ε) 内，但这个区间中包含大量不属于 X 的点。因此，它并不是开集。

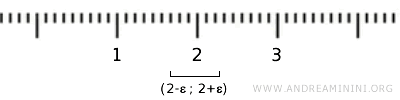
如果把 X 看作 \( \mathbb{R} \) 的子集，并采用“诱导拓扑”或“子空间拓扑”，那么它的开集只剩下空集和 X 本身。这样的拓扑虽然形式上成立，但没有太多研究价值。

对于有限集合，更有意义的做法是采用离散拓扑，即把 X 的每个子集都定义为开集。

这为研究有限空间的拓扑性质提供了更丰富的结构。