拓扑变换:从甜甜圈到咖啡杯的数学魔法
拓扑变换,是指一种让空间"变形"但不"破坏"的运算。它保持空间的关键特征,比如连通性与连续性,让我们得以理解那些看似奇妙的形状如何在数学上互相关联。
拓扑学就是研究这些变形的学科 - - 它不在意角度和长度,而关心的是"形状之间的本质关系"。在拓扑世界里,拉伸、弯曲、压扁都没问题,只要不撕裂、不粘合,一切皆有可能。
拓扑变换的核心特征
- 连续性
所有拓扑变换都必须连续。也就是说,小小的改变不会带来突然的跳跃 - - 输入轻微变动,输出也会平滑地跟着变化。 - 连通性与邻近性
在拓扑变换中,空间中点与点的关系被保留下来。如果两个点原本靠得很近,变形后它们依然紧密相连。 - 形变而不撕裂
想象一下:甜甜圈可以被"揉捏"成咖啡杯 - - 因为两者都有一个孔。这就是拓扑变换的魅力所在:形状变了,结构却没变。
应用: 拓扑变换不仅是纯数学的概念,在结理论、代数拓扑、甚至物理学中都有广泛应用,用于研究在连续变形下保持不变的性质。
常见的拓扑变换类型
不同的拓扑变换关注的重点不同,有的强调可逆性,有的强调连续变形的过程。
- 同胚映射(Homeomorphism)
同胚是拓扑学的基石。它是可逆且连续的变换,可以将一个空间平滑地变形成另一个,再无损地还原。例如,"杯子变甜甜圈"就是经典同胚。 - 同伦(Isotopy)
同伦可以理解为"连续的同胚过程"。比如一根打了结的绳子被慢慢移动或旋转,只要不拉紧或松开,整个过程中的每一步都是一次同伦。 - 同调变形(Homotopy)
同调描述函数之间的平滑变形。例如拉伸弹簧时,从松弛到拉直的每个形态都是同调的。相比同胚,同调的限制更宽松。 - 微分同胚(Diffeomorphism)
微分同胚不仅连续,还要求可微。它常用于研究光滑曲面,比如把一个球体平滑地拉成长椭球。
这些变换让我们从不同角度理解"空间的形变",也揭示了拓扑结构背后的数学之美。
几何变换 vs 拓扑变换
很多人会问:拓扑变换和几何变换到底有何不同?其实,区别就在于"在意什么"。
- 几何变换
关注的是形状、角度和距离。例如平移、旋转、镜像、缩放 - - 它们保持物体的几何比例。例如,旋转不会改变长度和角度,只会改变方向。
- 拓扑变换
则关注形状的"连通结构"。距离、角度都可以改变,只要不撕裂或粘合,一切都被允许。例如,甜甜圈和咖啡杯在拓扑上是"等价"的 - - 因为它们都有一个孔。
换句话说,几何变换注重精准的度量,而拓扑变换在乎的是"结构不变"。
既是几何又是拓扑的变换
有些变换既保留几何特征(如角度、长度、形状),又保持拓扑特征(如连通性与连续性)。
- 等距变换(Isometry)
平移、旋转、反射都属于等距变换。它们不改变点与点之间的距离,因此既是几何变换,也是拓扑变换。它们同时满足连续性与可逆性。
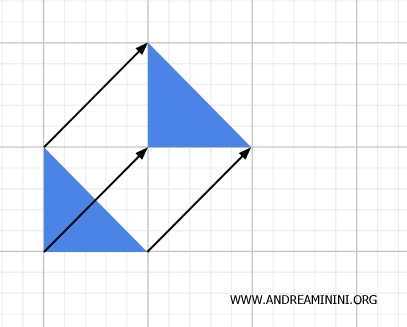
- 相似变换(Similarity)
相似变换可以改变物体大小,但保持形状比例。例如放大或缩小图形时,角度与相对比例保持不变。这类变换兼具几何与拓扑特征。
因此,几何与拓扑并不是完全分离的两个世界。某些变换既具有几何的"精准",又拥有拓扑的"灵活"。
结语: 从甜甜圈到咖啡杯,从旋转到拉伸,拓扑学让我们重新认识"形状"的本质 - - 它提醒我们,形式可以变化,但结构才是永恒的。