集合内部与交集的关系

在拓扑空间中，两个集合 $A$ 与 $B$ 的内部的交集，等于它们交集的内部 $ \text{Int}(A \cap B) $ $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$

这一结论表明，先分别求集合 $A$ 和集合 $B$ 的内部，再对所得结果取交集，与先对 $A$ 和 $B$ 取交集再求其内部，最终得到的集合完全相同。

换句话说，如果我们收集所有位于 $A$ 内部的点，以及所有位于 $B$ 内部的点，然后找出它们的公共部分，那么得到的点集正好就是集合 $A \cap B$ 的内部。

为了更好地理解这一性质，需要明确以下两个基本概念：

集合的内部（$\text{Int}(A)$）：由集合 $A$ 中的所有内部点组成。每一个内部点都具有这样的性质：在该点周围可以找到一个开邻域，使其完全包含在集合 $A$ 中，而不接触集合的边界。
交集（$\cap$）：由同时属于集合 $A$ 和集合 $B$ 的所有点构成的集合。

因此，对 $\text{Int}(A)$ 与 $\text{Int}(B)$ 取交集，得到的结果自然就是集合 $A \cap B$ 的内部。

一个直观的例子

设想两个部分重叠的圆形区域 $A$ 和 $B$。

集合 $A$ 的内部是去除边界后的整个圆盘区域，集合 $B$ 的内部同样如此。

两个集合的交集示意图

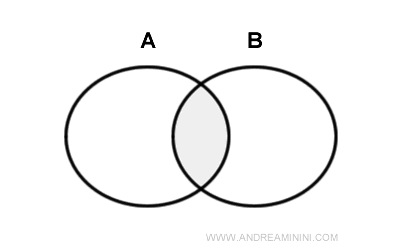
当我们取这两个内部区域的交集时，得到的区域正好对应于 $A$ 与 $B$ 重叠部分的内部，这与上述结论完全一致。

下面通过两个方向的包含关系，对这一结论进行说明。

1] 证明 $\text{Int}(A) \cap \text{Int}(B) \subseteq \text{Int}(A \cap B)$

若某点同时属于集合 $A$ 和集合 $B$ 的内部，则在该点周围一定存在一个开邻域，该邻域既完全包含在 $A$ 中，也完全包含在 $B$ 中。

因此，这个邻域必然包含在 $A \cap B$ 中，从而说明该点属于集合 $A \cap B$ 的内部。

设 $x \in \text{Int}(A) \cap \text{Int}(B)$，则 $x \in \text{Int}(A)$ 且 $x \in \text{Int}(B)$。

根据内部的定义，存在两个开邻域 $U$ 和 $V$，使得 $x \in U \subseteq A$，以及 $x \in V \subseteq B$。

令 $W = U \cap V$。由于 $U$ 与 $V$ 均为开集，$W$ 也是开集，并且包含点 $x$。

又因为 $W \subseteq U \subseteq A$，且 $W \subseteq V \subseteq B$，可得 $W \subseteq A \cap B$。

因此，$x \in \text{Int}(A \cap B)$。

2] 证明 $\text{Int}(A \cap B) \subseteq \text{Int}(A) \cap \text{Int}(B)$

反过来，若某点属于集合 $A \cap B$ 的内部，则存在一个完全包含在 $A \cap B$ 中的开邻域。

这意味着该邻域同时包含在集合 $A$ 和集合 $B$ 中，因此该点既是 $A$ 的内部点，也是 $B$ 的内部点。

设 $x \in \text{Int}(A \cap B)$。则存在一个包含 $x$ 的开邻域 $W$，使得 $W \subseteq A \cap B$。

由于 $W \subseteq A \cap B$，可知 $W \subseteq A$，且 $W \subseteq B$。

因此，$x \in \text{Int}(A)$ 且 $x \in \text{Int}(B)$。

综合以上两个方向的包含关系，可以得出最终结论：

\[ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) \]

至此，该性质的说明与证明全部完成。