以开矩形为基的拓扑

在平面 R² 中，我们可以用开矩形来建立一套拓扑基，从而描述什么样的集合算是“开”的。开矩形由两个坐标轴上的开区间组成，是理解欧氏平面局部结构的一种直接而高效的方式。

在这一拓扑中，开矩形是最基本的构件。所有的开集都可以看作若干开矩形的并。这让整个拓扑结构既简单又直观。

更具体地说，对于集合 \( U \subseteq \mathbb{R}^2 \)，如果每个属于 \( U \) 的点 \( (x, y) \) 都能被某个完全落在 \( U \) 内的开矩形包围，那么 \( U \) 就是开集。这正是拓扑基的核心思想。

因此，用开矩形作为基，可以构造出与我们熟悉的标准开球拓扑完全一致的欧氏平面拓扑。

$$ B = \{ (a, b) \times (c, d) \mid a< b,\ c

这里的 \( a, b, c, d \) 是满足 \( a< b \) 和 \( c

虽然标准拓扑通常以开球为基，但使用开矩形同样可以得到完全相同的开集结构。这说明拓扑关注的是集合之间的关系，而不是邻域的具体形状。

说明：拓扑基不唯一。只要生成的开集族相同，所定义的拓扑就完全一致，无论使用开球还是开矩形。

开矩形示例

在 \( \mathbb{R}^2 \) 中，开矩形是最常见的基本开集。它由两个开区间取笛卡尔积得到。

例如，考虑 \( x \) 轴上的开区间 \( (1, 3) \) 和 \( y \) 轴上的开区间 \( (2, 4) \)。

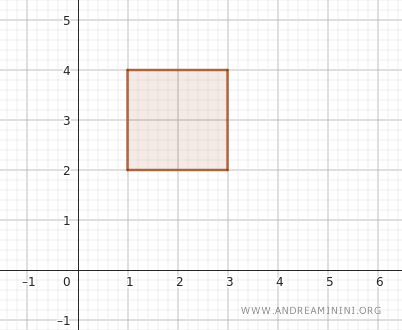
这个开矩形包含所有满足 \( 1

用数学形式表达，就是 \( (1, 3) \times (2, 4) \)。

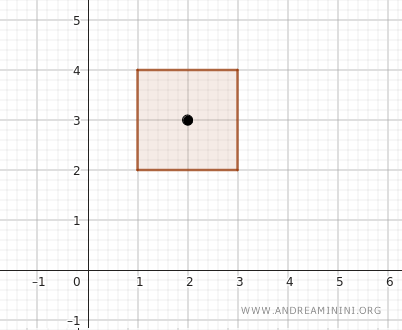
例如点 \( (2, 3) \)，它的横坐标介于 1 和 3 之间，纵坐标介于 2 和 4 之间，自然属于这个开矩形。

说明：开矩形不包含其边界。像 \( (1, y) \)、\( (3, y) \)、\( (x, 2) \) 和 \( (x, 4) \) 这样的边界点，都不在开矩形内部。