豪斯多夫空间（T₂ 空间）

豪斯多夫空间是拓扑学中最基本、也最实用的分离空间概念之一。如果一个空间能够让任意两个不同的点通过互不相交的开邻域加以区分，那么我们就称它为豪斯多夫空间。这样的空间在分析、几何以及更广泛的数学领域中都扮演着非常重要的角色。

简单来说，只要给定两个不同的点 \( x \) 和 \( y \)，总能找到两个开邻域 \( U \) 和 \( V \)，使得它们互不重叠，即 \( U \cap V = \emptyset \)。这保证了空间对"点的分离"具有非常良好的表现形式。

之所以如此重要，是因为豪斯多夫空间能够保证极限点和序列收敛等概念的唯一性。这一点对于分析学至关重要，让许多证明和推导更加自然可靠。

豪斯多夫空间有一个最核心的性质：每个单点集合都是闭集。换句话说，只要把空间中某个点拿掉，剩下的部分一定构成一个开集。

示例

示例 1：实数轴与标准拓扑

实数轴 \(\mathbb{R}\) 是最常见的例子，它采用的是标准拓扑。

在这种拓扑中，单点集合并不是开集，因为开集必须包含某个开区间，而单点无法做到这一点。

说明：任意两个实数之间都有无穷多个点，所以单点集合 \( \{x\} \) 不可能包含任何非平凡区间，也就不可能构成开集。

不过，单点的补集 \( \mathbb{R} \setminus \{x\} \) 却始终是开集。

因此单点集合都是闭集。

此外，实数轴也是典型的豪斯多夫空间。任意两个不同的点总能找到互不相交的开区间，将它们清晰地分离开来。

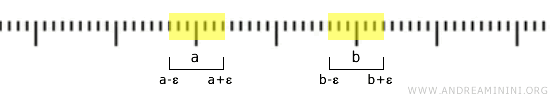
例如，如果 \( a < b \)，可以选取 \( (a-\epsilon, a+\epsilon) \) 和 \( (b-\epsilon, b+\epsilon) \)，只要 \( a+\epsilon < b-\epsilon \)，两个区间就不会相交。

这与豪斯多夫空间的定义完全吻合。

示例 2：离散拓扑空间

再来看集合 X = {1,2,3}，并赋予其离散拓扑。

在离散拓扑中，所有子集都是开集。从空集到全集，共有 \( 2^3 = 8 \) 个开集。

离散拓扑空间一定是豪斯多夫空间，因为任意两个不同的点，用各自的单点集合就可以把它们区分开来。

例如：

$$ \{1\} \cap \{2\} = \emptyset $$

因此它们的邻域互不重叠。

相比之下，标准拓扑只有满足邻域条件的集合才是开集，因此并不是所有子集都能称为开集。

补充说明

豪斯多夫空间的一个关键优势是，它让序列的收敛行为十分明确：

• 在豪斯多夫空间中，序列的极限是唯一的
  如果一个序列在豪斯多夫空间中收敛，那么它不可能同时收敛到两个不同的点。这是豪斯多夫分离性质的直接推论。

简要说明：若序列 x_n 同时落在点 x 与点 y 的邻域中，那么这两个邻域必然有交集，这与豪斯多夫空间中不同点必须拥有不相交邻域的要求矛盾。因此极限必须唯一。

这一性质使豪斯多夫空间在处理极限、连续性与分析结构时特别可靠，因而成为拓扑学中的标准要求之一。