离散拓扑

离散拓扑 T 是集合 X 上可以定义的最大拓扑结构，因为它包含了 X 的所有子集。

换句话说，在离散拓扑中，开集族 T 就是 X 的所有可能子集的集合。这意味着 X 的每个子集都是一个开集。

因此，X 中的每个元素都被视为"开"的，也就是说，每个点都是彼此独立的、互不相连的。

在这种拓扑结构中，不存在"距离"或"邻近"的概念，元素之间的关系完全自由，不受任何约束。

注意：集合 X 上的一个拓扑，是由 X 的若干子集（称为"开集"）构成的集合，必须满足以下条件：

"离散"这个名字很形象地反映了这种结构的特点：每个元素都是完全分开的，没有任何连续或渐变的联系。

离散拓扑是集合上可定义的最大拓扑结构，因为没有任何其他拓扑能包含更多的开集。它已经包括了所有可能的子集。

注意：这些条件为研究空间中点与点之间的"邻近性"和"连续性"提供了基础，使我们能够讨论空间中点在不间断情况下的连接，也就是连续性。

离散拓扑的关键性质

离散拓扑有一个非常重要的特征：

在离散拓扑中，每个子集既是开集，又是闭集。

这是因为离散拓扑把所有子集都看作开集，那么每个子集的补集自然也是开集。

在拓扑学中，如果一个集合的补集是开集，那么它就是闭集。

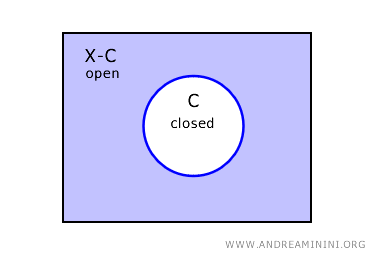
闭集的补集

因此，在离散拓扑中，每个子集同时是开集与闭集。这种性质让所有子集都成为开闭集。

注意：这种特性不仅适用于单个点，而是对所有子集都成立。每个点本身是开集，任意点的组合也是开集。由于补集依然是空间的子集，因此也是开集，从而每个子集同时是闭集。

我们通过一个具体的例子来看看离散拓扑的样子。设集合 X 包含三个元素：

$$ X = \{a, b, c\} $$

X 的幂集，也就是它的所有可能子集如下：

在离散拓扑中，以上每个子集都被视为开集。

因此，X 上的离散拓扑 $T$ 可写为：

$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$

由定义可知，X 的每个子集都是开集。

注意：这确实是一个拓扑结构，因为它包含 X 和空集，而且任意开集的并集与交集仍属于 T。由于所有子集都是开集，X 的元素之间不存在任何关于邻近性或连续性的限制。

例如，子集 $ \{ a \} $ 是开集，同时它的补集 $ X / \{a\} = \{b, c\} $ 也是开集，因此 $ \{ a \} $ 也是闭集。

这说明在离散拓扑中，任何子集都是开闭集。

同样的结论适用于其他所有子集。