子空间拓扑

在拓扑学中，如果已知拓扑空间 \( (X, T) \)，其中 \( X \) 是一个集合，\( T \) 是定义在其上的开集族，那么当我们取一个子集 \( Y \subseteq X \) 时，可以在 \( Y \) 上构造出一个新的拓扑。这个拓扑称为子空间拓扑，定义为：\[
T_Y = \{ U \cap Y \mid U \in T \} \] 换句话说，子空间中的开集就是原空间的开集与 \( Y \) 的交集，也被称为诱导拓扑。

因此，只要一个集合 \( V \subseteq Y \) 能写成 \( U \cap Y \)，其中 \( U \) 是原空间中的开集，那么 \( V \) 在子空间拓扑下就是开集。

$$ V_{open \ in \ Y} = U \cap Y $$

同理，子空间中的闭集也都能写成 \( C \cap Y \)，其中 \( C \) 是原空间中的闭集。

$$ V_{closed \ in \ Y} = C \cap Y $$

这说明，所谓拓扑子空间，就是原空间的一个子集，并以原拓扑自然诱导出的方式获得自身的拓扑结构。

注：子空间中的开或闭性质不一定在原空间中保持不变。有些集合在 \( Y \) 中是开集却在 \( X \) 中是闭集，也可能同时在两个空间中都是开集或都是闭集。还有一种特殊情况是闭开集，即同时为开与闭的集合。后面的示例将展示这种现象。

具体示例

以实数集 \( \mathbb{R} \) 配以标准拓扑为例，开集是各种开区间。

取子集 \( Y = [0,1] \)，并考虑 \( Y \) 上的子空间拓扑。

根据定义，子空间中的开集都可以写成：

$$ U \cap [0,1] $$

其中 \( U \) 是 \( \mathbb{R} \) 中的开集。

例如，区间 (-1,0.5) 是实数中的开集。

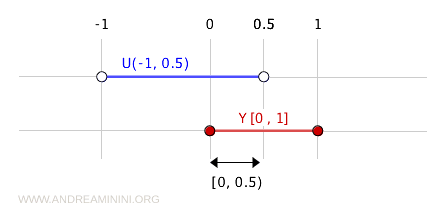
将它与 \( Y \) 取交，得到：

$$ (-1,0.5) \cap [0,1] = [0,0.5) $$

于是区间 \( [0,0.5) \) 在子空间中是开集。

而区间 \( [0,0.5] \) 在 \( Y \) 中是闭集，因为它可以写成原空间的闭集与 \( Y \) 的交：

$$ [-1,0.5] \cap [0,1] = [0,0.5] $$

由此可见，子空间拓扑完全由这种"与开集取交"的方式确定。

注：一些在实数标准拓扑中并非开集的区间，如 [0,a) 或 (a,1]（0

也有一些集合在原空间与子空间中都是开集，如 (0.2,0.8)。

一些集合在二者中都是闭集，如 [0.2,0.8]。

特别地，在子空间 \( Y=[0,1] \) 中，区间 \( [0,1] \) 同时为开与闭，是一个典型的闭开集。

• 为什么它是开集
  取原空间中的开集 \( U=\mathbb{R} \)，则：$$ U \cap Y = \mathbb{R} \cap [0,1] = [0,1] $$ 因此 \( [0,1] \) 在子空间中是开集。
• 为什么它是闭集
  取原空间中的闭集 \( C=[0,1] \)，则：$$ C \cap Y = [0,1] \cap [0,1] = [0,1] $$ 因而 \( [0,1] \) 在子空间中也是闭集。

  注：还可以从补集角度理解。\( [0,1] \) 在 \( Y \) 中的补集为空集，而空集在任何拓扑中都是开集，因此其补集为闭集，说明 \( [0,1] \) 在子空间中确实是闭集。

综上，区间 \( [0,1] \) 在子空间拓扑 \( Y=[0,1] \) 中同时具备开与闭的特征，是一个标准的闭开集。

示例 2

先来看实数集 \(\mathbb{R}\) 的标准拓扑。在这种拓扑结构下，所有的开区间 (a,b) 都是开集，这是我们比较熟悉的情况。

整数集 \(\mathbb{Z}\) 是 \(\mathbb{R}\) 的一个典型子空间，而它之所以能形成子空间拓扑，是因为每个整数都能用某个开区间与 \(\mathbb{Z}\) 的交集来"选取"出来。

例如：

$$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

同理，任意整数都能以类似方式得到。因此，在子空间拓扑下，每个整数都是开集，整数集的任意子集也都是开集。

例如，要得到 {6,7,8}，只需取：

$$ (5.5,8.5) \cap \mathbb{Z} = \{ 6,7,8 \} $$

由这里可以直观地看出，\(\mathbb{Z}\) 从 \(\mathbb{R}\) 继承的子空间拓扑恰好就是离散拓扑。

注：虽然 \(\mathbb{Z}\) 的离散拓扑不直接由 \(\mathbb{R}\) 的标准拓扑定义而成，但两者在 \(\mathbb{Z}\) 上诱导的结构完全一致。

示例 3

接下来将视角扩展到三维空间。考虑 \(\mathbb{R}^3\) 及其标准拓扑，开集由开球及其并集组成。

单位球面定义为：

$$ S^2 = \{ (x,y,z) \mid x^2+y^2+z^2 = 1 \} $$

当我们把 \( S^2 \) 看作 \(\mathbb{R}^3\) 的子集时，它自然继承了一套拓扑，这就是它的子空间拓扑：

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ 在 } \mathbb{R}^3 \text{ 中为开集} \} $$

也就是说，只有当 \( V \subseteq S^2 \) 能写成 \( U \cap S^2 \)（其中 \( U \) 是 \(\mathbb{R}^3\) 中的开集）时，\( V \) 才在球面上是开集。

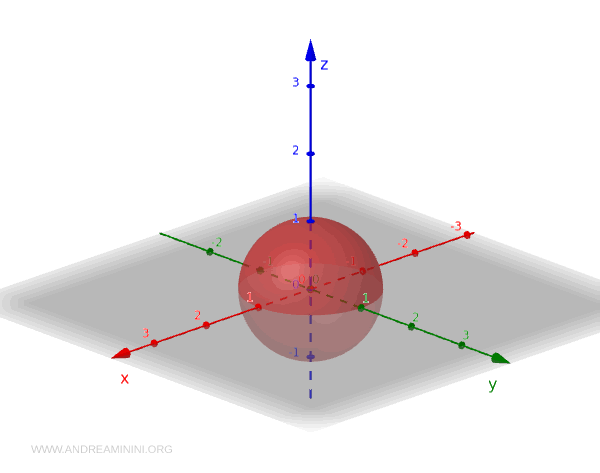
下面举几个直观的例子：

• 球面整体作为开集
  若取开集 \( U = \{ (x,y,z) \mid x^2+y^2+z^2 < 2 \} \)，则 $$ U \cap S^2 = S^2 $$ 因为球面上所有点都满足 \( 1 < 2 \)。于是，球面在自身的子空间拓扑中就是开集。
• 球面的局部区域
  若取 \( U = \{ (x,y,z) \mid x^2+y^2+z^2 =1,\ z>0 \} \)， 则 $$ U \cap S^2 = \{ (x,y,z) \in S^2 \mid z>0 \} $$ 这给出了球面的上半球，显然是一个自然的开集。
• 开集的封闭性
  空集与整个球面都是开集； 有限交仍为开集； 任意并仍为开集。 这些性质与原空间保持一致。

可以看到，球面作为子空间时，所有开集都来源于球面与三维开集的相交。

子空间拓扑的核心性质

总结子空间拓扑的基本特征：

1. 开集来源明确
   所有开集都由原空间开集与 \( Y \) 的交集构成。
2. 空集与整体必然为开
   因为 \( \emptyset = \emptyset \cap Y \) \( Y = X \cap Y \)。
3. 有限交保持开性
   若 \( V_i = U_i \cap Y \)，则 $$ \bigcap V_i = \left( \bigcap U_i \right) \cap Y $$ 原空间开集的有限交仍为开。
4. 任意并保持开性
   若 \( V_\alpha = U_\alpha \cap Y \)，则 $$ \bigcup V_\alpha = \left( \bigcup U_\alpha \right) \cap Y $$ 原空间开集的任意并仍为开。

补充说明

关于子空间拓扑，还有一些常见且实用的结论：

• 标准拓扑的一致性
  若 \( Y \subseteq \mathbb{R}^n \)，那么 \( Y \) 的标准拓扑与它从 \(\mathbb{R}^n\) 继承的子空间拓扑完全一致。

  示例：设 \( Y = [-1,0) \cup (0,1] \)。 由于 $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ 可见这两个区间在 \( Y \) 中都是开集，且互为补集，因此也都是闭集，是典型的闭开集。

• 子空间拓扑的基定理
  若 \( X \) 的拓扑基为 \( B_X \)，则 $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$ 构成 \( Y \) 的子空间拓扑的一组基。

以上内容为子空间拓扑的主要示例、性质及应用，为进一步深入学习拓扑结构奠定基础。