拓扑学中的连通性：空间的"整体感"

在拓扑学中，一个空间如果不能被划分成两个互不相交的开集，就称为连通空间。简单来说，连通性描述的是：在不离开空间的情况下，是否能从任意一点走到另一点。

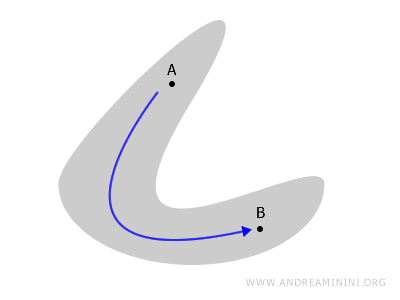
换个角度理解，连通性体现的是空间是否"是一整块"的。如果一个空间中所有部分都彼此相连，那它就是连通的；反之，如果被分隔成几块，那就不连通。

这是一个拓扑性质，因为它是通过开集来定义的。

连通性与连续性一样，是拓扑学的基础概念之一，也是理解"形状的本质"时不可或缺的工具。

在数学中，连通性帮助我们认识空间的整体结构，判断其中的各部分是如何相互关联的。通过它，我们可以对不同的空间进行分类、比较与分析。

一个直观的例子

想象一下，一个图形或立体模型。如果在其中任意两点 A 和 B 之间，都能画出一条始终留在空间内部的连续曲线，那么这个空间就是连通的。

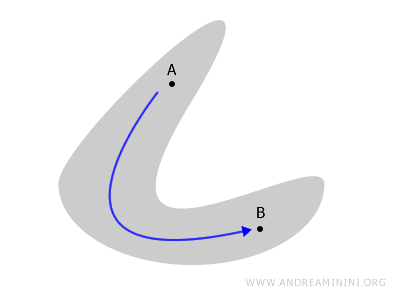
反之，如果空间的部分彼此隔离、互不相通，那这个空间就是非连通的。

比如下面这个例子中，空间被分成了两块，从 A 到 B 的任何路径都必须"走出去"，因此它是非连通的。

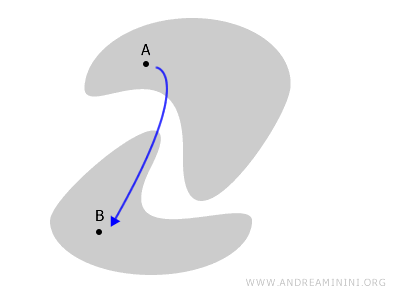
空间为何会不连通？

我们可以用一个生活化的比喻来理解：想象一栋建筑里有两个房间，中间隔着一堵墙。两个房间就像两个互不相交的开集，它们都不包含墙壁（边界），因此互不相连。

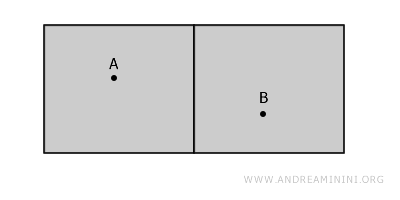
虽然房间看上去靠得很近，但它们并不连通，因为从 A 到 B 的任何路径都要穿过墙，而墙并不属于空间的一部分。

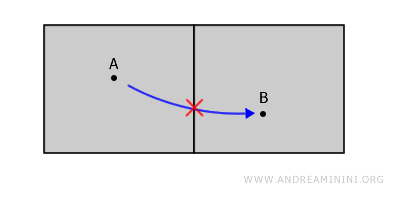
由此可见，开集的边界并不包含在开集本身中，这是判断连通性的关键之一。

局部连通性：空间内部的"小连通"

如果一个空间虽然整体上不连通，但其中每个点都属于某个连通的邻域，那么这个空间被称为局部连通的。

比如，下图展示的空间由两个分开的开集组成，看起来不连通。

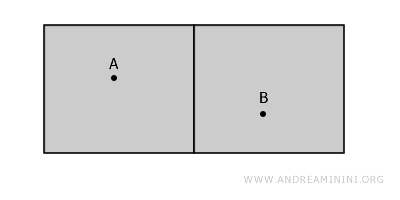
虽然整体上点 A 与点 B 之间无法连通，但在点 A 附近的小区域内，所有点之间都是相互连接的。这说明 A 点所在的局部是连通的。

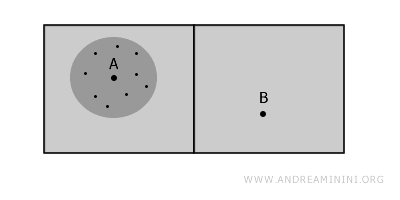
点 B 同样如此 - - 它所在的小范围内部也是连通的。

连通性的两种重要类型

在拓扑学中，最常讨论的两类连通性是：

• 拓扑连通性
  在拓扑学中，如果一个空间 $ X $ 不能被分割为两个既非空又互不相交的开集，并且这两个开集的并集恰好等于整个空间，那么我们称 $ X $ 是连通的。换句话说，连通空间无法被“切开”成两个彼此独立的部分。

  示例：区间 (-1, 1) 是连通的，而区间 (-1, 0) ∪ (0, 1) 则不是。因为可以找到两个非空且互不相交的开集 (-1, 0) 和 (0, 1)，它们的并集刚好覆盖整个空间。
  因此，这两个开集构成了该空间的一个分离（separation）。

• 道路连通性（或弧连通性）
  若一个拓扑空间中任意两点 A 和 B 之间都存在一条完全位于该空间内部的连续路径将它们连接起来，则称该空间是道路连通的。所有道路连通的空间必定是连通的，但连通空间不一定具有道路连通性。

  例如，在平面上画一个封闭图形。对于其中任意两点 A 和 B，都可以在图形内部画出一条连续曲线，将它们连接起来，而无需离开该区域或抬起笔。
  
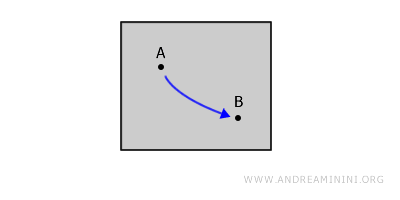
  弧连通与道路连通的区别：弧连通性与道路连通性类似，但要求路径是一一对应的，也就是说，路径不能自交，也不能重复经过同一点。

• 单连通性
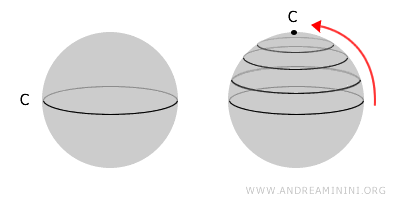
  如果空间中任意闭合曲线都能被连续地缩小为一个点，我们称该空间是单连通的。这意味着空间内部没有"洞"，是一个完全连成一体的整体。单连通空间一定连通，但连通空间不一定单连通。

  例如，球面是单连通的，因为表面上的任意闭合曲线都可以缩成一个点。而环面（像甜甜圈那样的形状）内部有一个洞，其中的一些曲线无法缩为一点，所以它是连通但非单连通的。
  
  
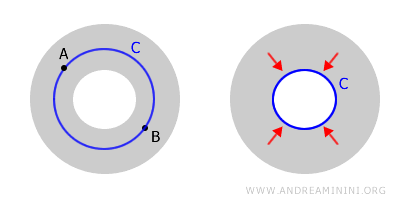
  这种连通但非单连通的空间被称为多连通空间，圆环区域就是典型的例子。

一个小结

理解连通性，就像理解空间的"整体感"。

• 在实数轴上，唯一连通的集合是连续的区间。
• 连通性告诉我们一个空间是否"连成一片"，而局部连通性揭示了这种结构在细节层面上的延续。

正是这种对"整体与局部"的把握，让拓扑学能在几何学、分析学乃至物理学中扮演重要角色。