既非开集也非闭集的集合

在拓扑学中，如果一个集合既不满足开集的条件，也不满足闭集的条件，那么它就被称为既非开集也非闭集的集合。

在某些拓扑空间中，可能出现这样的情况：一个集合既未被定义为开集，其补集也不是开集。

因此，该集合同样不能被视为闭集。

注意：在实数这一常见拓扑空间中，这类现象不太直观。不过在更加一般或复杂的拓扑结构中，它们是完全可能存在的。通过一个具体示例，可以更清晰地理解这一概念。

一个具体示例

设集合 X={a,b,c,d}，拓扑 T 所定义的开集为：{b}、{a,b}、{c,d}、{b,c,d}、{a,b,c,d} 和 Ø。

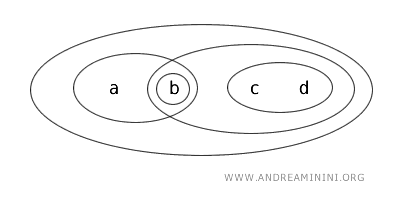
现在考察子集 {b,c}。

• 集合 {b,c} 不是开集，因为它并未在拓扑 T 中被列为开集。
• 同时，{b,c} 也不是拓扑 T 内任何开集的补集，因此不能视为闭集。

因此，在拓扑 T 中，{b,c} 既不是开集，也不是闭集。这类集合在更广泛的拓扑讨论中非常典型，有助于理解开集与闭集概念的边界。

其他类似情况也可以用相同的思路进行分析。