正规空间

正规性的核心在于分离能力。只要两个闭集没有共同元素，我们总能找到互不重叠的开邻域将它们隔开。这个性质是许多重要拓扑结论的基础，也常用于构造能够区分点或集合的连续映射。

一个直观的例子

考虑带标准拓扑的实数空间 \( \mathbb{R} \)，其拓扑由开区间 \( (a, b) \) 生成。

来看两个典型的闭集：

• \( A = \{0\} \)，单点集。
• \( B = [2, 3] \)，闭区间。

它们在标准拓扑下都是闭集，并且毫无交集。

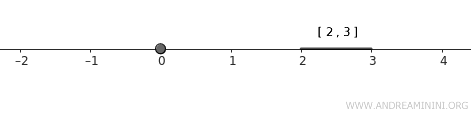
说明. 单点集 \( A \) 本身就是闭集，而闭区间 \( B \) 也自然是闭的。

下面的目标是找出两个完全不重叠的开集分别包含它们。

对于 \( A = \{0\} \)，可以选取开邻域 \( U = (-1, 1) \)。

$$ A \subset U = (-1,1) $$

对于闭区间 \( B = [2,3] \)，可以取开集 \( V = (1, 4) \)，它完整覆盖整个区间。

$$ B \subset V = (1,4) $$

显然，\( U \) 和 \( V \) 并不相交，这正是正规空间要求的分离特性。

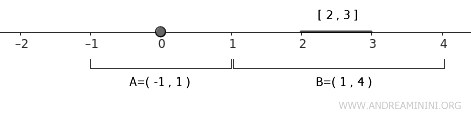
不仅在这个例子中，在实数轴上任何两个互不相交的闭集，都可以凭借同样的思路找到相应的不相交开集将它们分离。这也是实数轴的标准拓扑被称为正规拓扑的原因。

进一步理解正规空间

正规空间在拓扑学中扮演着重要角色。下面是几个常见结论：

• 实数轴 \( \mathbb{R} \) 的标准拓扑是正规拓扑
  它不仅能分离点和闭集（正则性），还能分离两个闭集，因此结构更强。
• 所有度量空间都是正规空间
  度量结构提供良好的分离性能，因此度量空间天然正规。
• 正规空间必定是正则空间
  正规性比正则性更强，是拓扑空间分离性质层级中的重要一环。

理解正规空间有助于掌握更多高级拓扑理论，例如乌雷松引理、Tietze 延拓定理等，它们都深受这种分离结构的支撑。