正则空间

从分离性质来看，正则空间比豪斯多夫空间更进一步。它不仅要求区分不同的点，还要求能将点与与之无关的闭集分开。

一个正则空间如果拥有可数基，那么根据乌里索恩度量化定理，它就能被赋予某种度量。这意味着空间结构良好且便于研究。

正则性为什么比豪斯多夫更强

豪斯多夫空间只关心两点之间是否能分开，而正则空间则更严格，要求点与闭集之间也能清晰区分。换句话说，正则性提升了空间的"辨识度"。

说明。正则空间不等同于正规空间。正规空间的要求更高，它必须能分离任意两个互不相交的闭集。因此，正规空间一定正则，但正则空间不一定正规。  

此外，正则性和豪斯多夫性彼此独立。一个空间可能正则但不豪斯多夫，也可能豪斯多夫却不正则。实际例子在拓扑文献中均有出现。

一个直观易懂的例子

最典型的正则空间例子就是实数直线 \( \mathbb{R} \) 配以通常拓扑。

取点 \( x = 2 \)，并考虑闭集：

\[ C = (-\infty, 0] \cup [5, \infty) \]

很明显，这个闭集并不包含点 \( x = 2 \)。

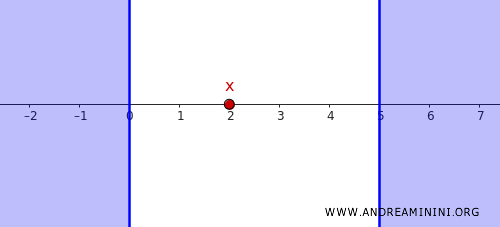
现在我们尝试把点和闭集"分开"。

因为 \( C \) 的补集是开集，我们可以在补集里找到一个包含 \( x \) 的开区间，例如：

\[ (0,5) \]

接着选取两个数：

\[ 0 < c < 2 < d < 5 \]

例如：

\[ c = 1,\quad d = 3 \]

由此可构造两个开集：

• \( U = (1,3) \)，它包含点 \( 2 \)。
• \( V = (-\infty,1) \cup (3,\infty) \)，它完全覆盖闭集 \( C \)。

显然，\( U \) 和 \( V \) 完全不相交，从而满足正则性的要求。

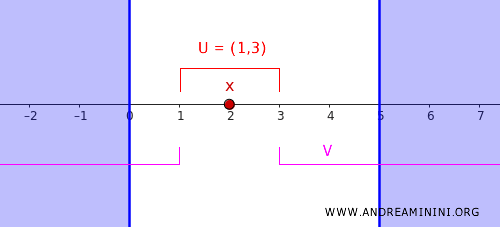
通过这个例子，我们能直观地看到正则性是如何通过开集来实现"点与闭集的分离"的。

进一步理解正则空间

• 分离公理体系中的角色
  在拓扑学中，分离公理用来衡量一个空间区分点与集合的能力。豪斯多夫性关注点与点的分离，正则性则扩展到点与闭集的分离。

  说明。豪斯多夫空间要求不同的点能被不相交的开集分开，正则空间要求一个点与不包含它的闭集也能被分开。这些性质展示了空间在结构上的"分辨率"。

正则空间是理解拓扑分离性质的重要一步，同时也是通向更强条件（如正规空间）的基础。