既开又闭的集合（Clopen Sets）

在拓扑学中，如果一个集合在某个拓扑下同时是开集和闭集，就被称为既开又闭的集合（clopen）。

这类集合之所以引人关注，是因为它们突破了我们对开集与闭集“互斥”的直觉认识，却又完全符合拓扑结构的逻辑，是理解空间结构时非常有价值的工具。

术语 “clopen” 由 “closed” 与 “open” 合并而来，用于概括这种特殊类型的集合。它兼具开集与闭集的性质，而出现这种情况的关键在于：集合本身及其补集必须同时为开集。

提示：在实数拓扑中，clopen 集极少出现，但在其他拓扑空间中却并不罕见。它们常被用来分析空间是否“连通”，在拓扑学理论中具有重要地位。

示例解析

考虑拓扑空间 X={a,b,c,d}，拓扑记为 T。

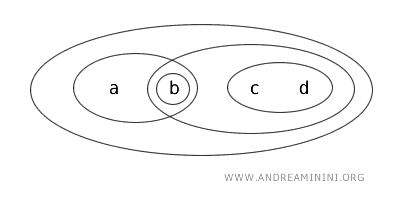
在拓扑 T 中，以下集合被定义为开集：{b}、{a,b}、{c,d}、{b,c,d}、{a,b,c,d} 和 ∅。

因此，{a,b} 显然是一个开集。

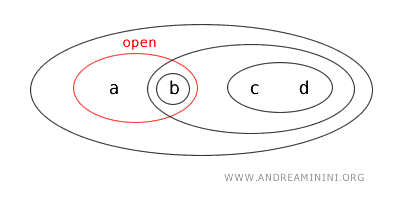
同时，{a,b} 恰好是 {c,d} 的补集：

$$ X - \{ c,d \} = \{a , b \} $$

由于开集的补集必然是闭集，可以得到：

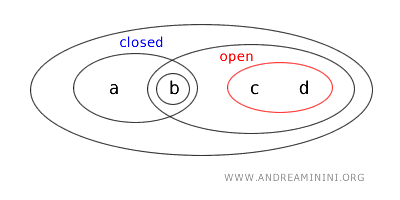
因此，{a,b} 兼具开集与闭集的性质，是一个 clopen 集。

为什么空集和全集总是 Clopen

无论拓扑如何变化，空集 ∅ 与全集 X 永远同时是开集和闭集，因此必然是 clopen 集。

根据开集的定义，空集和全集总是开集；根据闭集的定义，一个集合若其补集为开集，则该集合为闭集。将两者结合便可得到结论：

• 空集（∅）
  空集是开集，而其补集 X 也是开集，因此空集也是闭集，属于 clopen 集。
• 全集（X）
  全集为开集，而其补集 ∅ 也是开集，因此全集同样是闭集，也属于 clopen 集。

因此，在任意拓扑空间中，空集与全集始终是最基本且永远存在的 clopen 集。

理解 clopen 集不仅有助于把握拓扑空间的结构，还能为学习连通性和空间分解等更深层主题打下基础。