集合的闭包
在拓扑空间 \( X \) 中,集合 \( A \) 的闭包是指所有包含 \( A \) 的闭集的交集,通常记为 \( \text{Cl}(A) \)。
直观地说,集合 \( A \) 的闭包就是"刚好把 \( A \) 包住"的最小闭集。
任何包含 \( A \) 的闭集,都不可能比 \( \text{Cl}(A) \) 更小。
说明:这一性质直接源自定义。闭包通过对所有包含 \( A \) 的闭集取交而得到,因此可以理解为在拓扑意义下最紧密地围绕 \( A \) 的闭集,它由这些闭集中共同出现的元素组成。
用形式化语言表示,集合 \( A \) 的闭包为:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X : A \subseteq C \text{ 且 } C \text{ 在 } X \text{ 中是闭集} \} $$
其中,\( \bigcap \) 表示对所有满足条件的闭集 \( C \) 取交集。
因此,\( \text{Cl}(A) \) 不仅包含集合 \( A \) 本身,还包含 \( A \) 在空间 \( X \) 中的全部极限点。
说明:需要注意的是,闭包的概念更多反映的是空间 \( X \) 的拓扑结构,而不是集合 \( A \) 自身的特性。在不同的拓扑空间中,同一个集合的闭包可能会发生变化。
示例说明
在实数集 \( \mathbb{R} \) 上,考虑集合 \( A = (0, 1) \),并采用标准拓扑。
该集合表示不包含端点 0 和 1 的开区间。
在这种情况下,集合 \( A \) 的闭包为:
$$ \text{Cl}(A) = [0,1] $$
也就是说,闭包在原有区间的基础上补上了边界点 0 和 1,它们正是 \( A \) 的极限点。
说明:在 \( \mathbb{R} \) 的标准拓扑中,闭集等价于"包含全部极限点的集合"。例如,闭区间 [0,2] 与 [-1,1] 的交集是 [0,1]。$$ [0,2] \cap [-1,1]=[0,1] $$ 没有比 [0,1] 更小的闭集还能包含开区间 (0,1)。
示例 2
再看集合 \( A = [0, 1) \),仍然位于 \( \mathbb{R} \) 中并采用标准拓扑。
这是一个左端点包含、右端点不包含的区间。
它的闭包依然是:
$$ \text{Cl}(A) = [0,1] $$
原因在于,点 0 已经属于集合 \( A \),而点 1 虽不在 \( A \) 中,却是它的极限点,因此必须被加入闭包。
说明:这正体现了闭包"补齐极限点"的作用。例如,[0,2] 与 [-1,1] 的交集为 [0,1]。$$ [0,2] \cap [-1,1]=[0,1] $$
示例 3
现在保持集合 \( A = [0,1) \) 不变,但将拓扑空间 \( X \) 改为离散拓扑。
在离散拓扑中,空间的每一个子集既是开集,也是闭集。
- 开集
在离散拓扑下,\( X \) 的任意子集都是开集,因此 \( A \) 是开集。 - 闭集
同样地,任意子集的补集仍是 \( X \) 的子集,从而是开集,因此该子集本身也是闭集。
这意味着,在离散拓扑中,每个集合都是既开又闭的,称为开闭集。
因此,集合 \( A \) 已经是闭集,其闭包不需要添加任何新点:
$$ \text{Cl}(A) = [0,1) $$
说明:这一例子清楚地表明,闭包的结果会随着拓扑结构的改变而发生变化。
示例 4
考虑由点集 \( \{a, b, c\} \) 构成的拓扑空间 \( X \),并赋予其离散拓扑。
在这种拓扑下:
- \( \emptyset \) 与 \( \{a, b, c\} \) 是开集。
- 单点集 \( \{a\} \)、\( \{b\} \)、\( \{c\} \) 是开集。
- 任意有限组合,如 \( \{a, b\} \)、\( \{b, c\} \),同样是开集。
由于每个子集的补集仍是开集,因此所有子集同时也是闭集。
以集合 \( A = \{b, c\} \) 为例,它既是开集也是闭集。
按照闭包的定义,不需要引入任何新的元素,其闭包为:
\[ \text{Cl}(A) = \{b, c\} \]
说明:包含 \( A \) 的闭集只有 \( \{b, c\} \) 与 \( \{a,b,c\} \),它们的交集仍是 \( \{b, c\} \)。$$ \text{Cl}(A) = \{b,c\} \cap \{a,b,c\} = \{b, c\} $$ 因此在离散拓扑中,每个集合的闭包都等于它自身。
集合的闭包定理
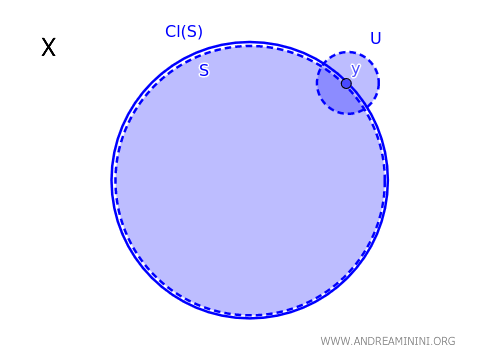
在拓扑空间 \( X \) 中,元素 \( y \) 属于子集 \( S \) 的闭包,记作 \( \text{Cl}(S) \),当且仅当任意包含 \( y \) 的开集 \( U \) 都与 \( S \) 有非空交集:\( y \in \text{Cl}(S) \iff \forall\, U \text{ 为开集且 } y \in U,\; U \cap S \neq \emptyset \)。
换一种更直观的说法:如果一个点 \( y \) 无论被多小的开集"包围",都无法与集合 \( S \) 完全分离,那么这个点就属于 \( S \) 的闭包。
这一判别定理在实际学习和应用中非常重要,它为判断某个点是否属于闭包提供了一个清晰而可操作的标准。
证明思路
- 必要性:若 \( y \in \text{Cl}(S) \),则按照闭包的定义,任何包含 \( y \) 的开集都必须与 \( S \) 相交。这正是闭包的核心特征:它不仅包含集合本身的点,还包含所有无法与集合"隔离开来"的极限点。
- 充分性:反过来,若任意包含 \( y \) 的开集都与 \( S \) 相交,那么 \( y \) 要么本身就在 \( S \) 中,要么是 \( S \) 的极限点。在这两种情况下,\( y \) 都必然属于 \( S \) 的闭包。
说明:该定理在拓扑学中被频繁引用,因为它将"开集"这一局部概念与"闭包"这一整体结构直接联系起来,是研究连续性、极限、收敛性等问题的基础工具。
示例
在实数集 \( \mathbb{R} \) 的标准拓扑下,考虑集合 \( A = (0, 2) \),这是一个简单而典型的开区间。
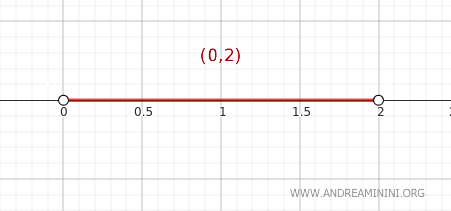
下面利用闭包定理判断某个点是否属于集合 \( A \) 的闭包 \( \text{Cl}(A) \)。
取点 \( y = 2 \)。
根据定理,只有当任意包含 \( y \) 的开集都与 \( A \) 相交时,\( y \) 才属于 \( \text{Cl}(A) \)。
- 考察包含 \( y \) 的开集:无论选取哪一个包含点 \( 2 \) 的开区间,例如 \( (1.9, 2.1) \)、\( (1.95, 2.05) \)、\( (1.99, 2.01) \),这些区间中总能找到属于 \( A = (0,2) \) 的点。
- 验证交集:由于所有这些开集都与 \( A \) 有非空交集,因此可以断定 \( y = 2 \) 属于 \( \text{Cl}(A) \)。
由此可知,点 \( y = 2 \) 满足闭包定理的条件,因此属于集合 \( A \) 的闭包。
$$ y \in \text{Cl}(A) $$
事实上,集合 \( A \) 的闭包是闭区间 \( \text{Cl}(A) = [0, 2] \),其中自然包含端点 2。
拓扑空间中的闭包性质
在理解闭包定理之后,有必要进一步了解闭包运算的一些基本性质,以及它与内部、补集等运算之间的关系。这些结论在拓扑学中具有基础性意义。
- 补集的内部与闭包的补集
集合 \( A \) 的补集的内部,等于 \( A \) 的闭包的补集:$$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$ - 补集的闭包与内部的补集
集合 \( A \) 的补集的闭包,等于 \( A \) 的内部的补集:$$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$
关键结论
下面总结若干关于集合闭包的常用结论,它们在理论推导和实际应用中都非常重要:
- 若 \( C \) 是闭集且 \( A \subseteq C \),则 \( \text{Cl}(A) \subseteq C \)
由于 \( \text{Cl}(A) \) 是包含 \( A \) 的最小闭集,而 \( C \) 本身已经是包含 \( A \) 的闭集,因此必有 \( \text{Cl}(A) \subseteq C \)。 - 若 \( A \subseteq B \),则 \( \text{Cl}(A) \subseteq \text{Cl}(B) \)
闭包运算具有单调性,集合之间的包含关系在取闭包后仍然保持。 - 集合 \( A \) 为闭集当且仅当 \( A = \text{Cl}(A) \)
一个集合是闭的,等价于它已经包含了自身的所有极限点。 - 闭包等于集合与其极限点的并集
若 \( A' \) 表示集合 \( A \) 的极限点集,则有:$$ \text{Cl}(A) = A \cup A' $$ - 幂等性
对集合反复取闭包不会产生新的点:$$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - 包含性
任意集合都包含于其闭包之中:$$ A \subseteq \text{Cl}(A) $$
后续将继续介绍更多与闭包相关的重要结论与应用。