拓扑学中的同胚映射

同胚（homeomorphism）是拓扑学中的一种映射，它要求函数既是双射，又连续，并且其逆函数也必须连续。

简单来说，同胚意味着一个空间可以通过连续的变形转化为另一个空间，而整个过程中不会出现“撕裂”或“粘合”。

换句话说，同胚让我们能够在不破坏或拼接任何部分的前提下，将一个空间平滑地“变形”为另一个空间。

例如，一个带把手的咖啡杯与一个甜甜圈（环面）在拓扑学中被认为是同胚的。因为它们可以通过连续的形变相互转化。

从拓扑学的角度看，它们是等价的形状，因为二者都具有一个“孔”：甜甜圈的中心空洞与咖啡杯把手的环状间隙。通过沿着杯把的方向调整形状，就能把咖啡杯变成甜甜圈。

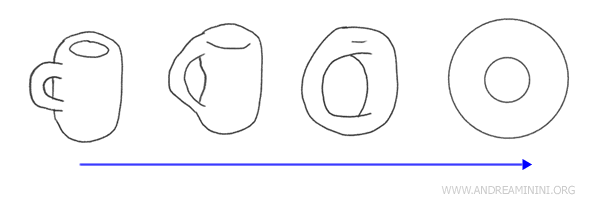
当两个拓扑空间之间存在同胚映射时，我们称它们为“同胚空间”。这意味着它们在拓扑结构上本质相同，即使在几何外观上可能不同。

同胚映射的基本特征

同胚映射具备以下几个核心特征：

• 双射性
  它在两个空间的元素之间建立一一对应关系，确保每个元素都有唯一对应，反之亦然。
• 连续性
  同胚映射必须是连续的，也就是说输入的微小变化只会引起输出的微小变化。
• 逆函数的连续性
  同胚的逆函数也必须连续，这样才能保证该变换可逆且平滑。
• 保持拓扑性质
  同胚保持空间的拓扑性质，如连续性、连通性和紧致性。也就是说，原空间的结构关系在变换后依然得到保留。

简而言之，同胚是两个拓扑空间 \(X\) 和 \(Y\) 之间的一个连续、可逆且逆函数也连续的映射。这样的映射会完整保留空间的拓扑特征。

换句话说，同胚是一种“重塑”空间的方式，可以在不撕裂或拼接的情况下把一个空间变形成另一个空间，是两种形状或空间之间的一种“完美对应”。

回顾一下拓扑学中连续性的定义：

设 \(X\) 与 \(Y\) 是两个拓扑空间。若对 \(Y\) 中任意开集 \(V\)，其原像 \(f^{-1}(V)\) 在 \(X\) 中也是开集，则称函数 \(f: X \to Y\) 为连续函数。

换句话说，在拓扑学中，连续函数在映射时会“保持”开集的结构特征。

因此，拓扑意义下的连续性是数学分析中连续性概念的推广与抽象化。

注意：在数学分析中，连续性依赖于点之间的距离；而在拓扑学中，它依赖于开集的结构，因此更一般，不需要距离的概念。

一个直观的例子

我们用开集来直观说明连续性和同胚的概念。

设两个拓扑空间 \(X = \{a, b, c, d\}\) 与 \(Y = \{1, 2\}\)。

• 在空间 \(X\) 中，开集为：\(\{\}, \{a\}, \{a, b\}, \{a, b, c, d\}\)。
• 在空间 \(Y\) 中，开集为：\(\{\}, \{1\}, \{1, 2\}\)。

若函数 \(f: X \rightarrow Y\) 满足对 \(Y\) 中的每个开集，其原像在 \(X\) 中也是开集，则 \(f\) 为连续函数。

定义函数 \(f: X \rightarrow Y\)：

\(f(a) = 1\)，\(f(b) = 1\)，\(f(c) = 2\)，\(f(d) = 2\)。

我们可以用圈出的开集来直观表示函数 \(f\) 与两个空间的关系。

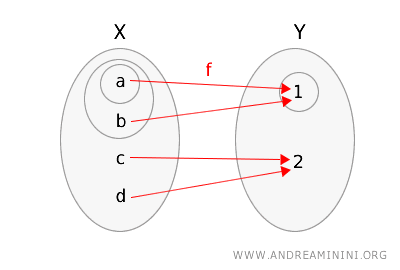
验证其是否满足拓扑连续性的定义：

• 取 \(Y\) 中的开集 \(\{1\}\)，其原像为 \(f^{-1}(\{1\}) = \{a, b\}\)，这是 \(X\) 中的开集。
• 取 \(Y\) 中的开集 \(\{1, 2\}\)，其原像为 \(f^{-1}(\{1, 2\}) = \{a, b, c, d\}\)，这也是开集。

因此，\(Y\) 中每个开集的原像在 \(X\) 中都是开集，说明该函数是连续的。

注意：空集在任何拓扑空间中都是开集，因此这里省略。

现在考虑另一函数 \(g: X \rightarrow Y\)：

\(g(a) = 1\)，\(g(b) = 1\)，\(g(c) = 1\)，\(g(d) = 2\)。

同样用圈出的开集表示函数 \(g\) 与空间的对应关系。

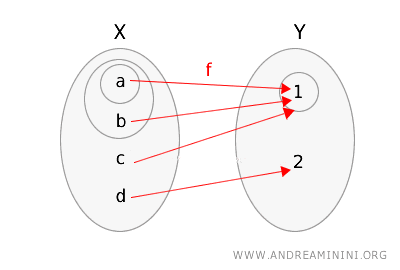
检查其是否满足连续性定义：

• 取 \(Y\) 中的开集 \(\{1\}\)，其原像为 \(g^{-1}(\{1\}) = \{a, b, c\}\)，该集合在 \(X\) 中不是开集。

由于存在至少一个开集（此处为 \(\{1\}\)）的原像在 \(X\) 中不是开集，因此函数 \(g\) 不连续。

总结：若目标空间 \(Y\) 的每个开集在原空间 \(X\) 中的原像都是开集，则函数连续；反之则不连续。在第一个例子中，函数 \(f\) 连续；在第二个例子中，函数 \(g\) 不连续。

同胚的定义

设 \( X \) 与 \( Y \) 为两个拓扑空间。若存在双射函数 \( f: X \to Y \) 及其逆函数 \( f^{-1}: Y \to X \)，且 \( f \) 与 \( f^{-1} \) 均连续，则称 \( f \) 为同胚映射，并称 \( X \) 与 \( Y \) 同胚，记作 \( X \cong Y \)。

同胚空间也称为拓扑等价空间。

这意味着什么？

同胚或拓扑等价表示两个空间在拓扑意义上“本质一致”，尽管它们的几何形状可能不同。

这个定义突出了同胚映射的关键条件：

1. 双射性：函数 \( f: X \to Y \) 必须是一一对应且满射。
2. 函数 \( f \) 的连续性：\(Y\) 中任意开集的原像在 \(X\) 中必须是开集。
3. 逆函数 \( f^{-1} \) 的连续性：\(X\) 中任意开集的原像在 \(Y\) 中也必须是开集。

例子：想象把一张纸卷成圆柱。圆柱面和平面是同胚的，因为它们可以通过“卷起”或“展开”的连续变形互相转化，不需要撕裂或粘合。拓扑结构（开集的关系）保持不变，尽管几何形状不同。

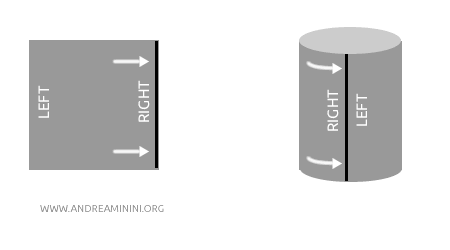
需要注意的是，连续且双射的函数 \( f \) 并不一定保证其逆函数 \( f^{-1} \) 也是连续的，除非 \( f \) 同时还是一个开映射。

换句话说，若函数 \( f \) 连续且双射，这并不必然意味着它的逆函数连续，因此不能直接称其为同胚。

在拓扑学中，若函数 \( f: X \rightarrow Y \) 使得 \(Y\) 中每个开集的原像在 \(X\) 中是开集，则称 \(f\) 连续。

但这并不意味着 \(f\) 将 \(X\) 中的每个开集都映射为 \(Y\) 中的开集。

要使逆函数 \( f^{-1} \) 也连续，\(f\) 必须不仅连续且为开映射。

例 1

我们先来看以下两个拓扑空间：

• \( X = (a, b) \)，其拓扑为 \( T_X = \{\emptyset, \{a\}, \{b\}, X\} \)。
• \( Y = (1, 2) \)，其拓扑为 \( T_Y = \{\emptyset, Y\} \)。

定义函数 \( f: X \to Y \)，令 \( f(a) = 1 \)，\( f(b) = 2 \)。

函数 \( f \) 显然是双射的，因为 \( X \) 中的每个元素都与 \( Y \) 中的一个元素一一对应，反之亦然。

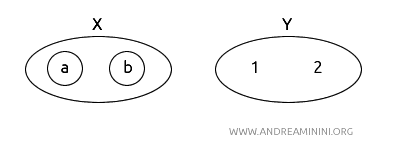
说明：图中用圆圈表示开集。例如，在 \( X \) 中，\(\{a, b\}\)、\(\{a\}\) 和 \(\{b\}\) 都是开集；而在 \( Y \) 中，只有 \(\{1, 2\}\) 是开集。按定义，空集在任何拓扑中都是开集，这里为简洁起见未画出。

下面我们分析函数 \( f \) 及其逆函数 \( f^{-1} \) 的连续性。

• 函数 \( f \) 的连续性
  要判断 \( f \) 是否连续，需要检查 \( Y \) 中每个开集的原像在 \( X \) 中是否为开集。\( Y \) 的开集为 \(\emptyset\) 和 \(Y\)：
  • \( f^{-1}(\emptyset) = \emptyset \)，在 \( T_X \) 中为开集；
  • \( f^{-1}(Y) = X \)，在 \( T_X \) 中也是开集。
  因此，\( f \) 是连续的。
• 逆函数 \( f^{-1} \) 的连续性
  逆函数 \( f^{-1}: Y \to X \) 定义为 \( f^{-1}(1) = a \)，\( f^{-1}(2) = b \)。 检查其连续性时，我们需要验证 \( X \) 中每个开集的原像在 \( Y \) 中是否为开集。\( X \) 的开集为 \(\emptyset\)、\(\{a\}\)、\(\{b\}\) 和 \(X\)：
  • \( f^{-1}(\emptyset) = \emptyset \)，在 \( T_Y \) 中为开集；
  • \( f^{-1}(\{a\}) = \{1\} \)，不是开集，因为在 \( T_Y \) 中，包含 1 的唯一开集是 \( Y \)；
  • \( f^{-1}(\{b\}) = \{2\} \)，同样不是开集；
  • \( f^{-1}(X) = Y \)，在 \( T_Y \) 中为开集。
  由于 \(\{a\}\) 和 \(\{b\}\) 的原像在 \( Y \) 中都不是开集，所以 \( f^{-1} \) 不连续。

因此，函数 \( f \) 虽然是双射且连续，但其逆函数 \( f^{-1} \) 不连续，因此 \( f \) 不是同胚映射。

这个例子说明，即使一个函数既双射又连续，也不能保证它的逆函数同样连续。

说明：在此例中，\( f^{-1} \) 不连续的原因在于 \( X \) 和 \( Y \) 的拓扑结构不同。\( X \) 的拓扑较“细”，拥有更多开集（如 \(\{a\}\)、\(\{b\}\)），而 \( Y \) 的拓扑较“粗”，仅包含 \(\emptyset\) 与 \(Y\)。

例 2

再来看一组不同拓扑的空间：

• \( X = (a, b) \)，其拓扑为 \( T_X = \{\emptyset, \{a\}, X\} \)。
• \( Y = (1, 2) \)，其拓扑为 \( T_Y = \{\emptyset, \{1\}, Y\} \)。

定义函数 \( f: X \to Y \)，令 \( f(a) = 1 \)，\( f(b) = 2 \)。

同样地，\( f \) 是双射，因为 \( X \) 中的每个元素都唯一对应于 \( Y \) 中的一个元素。

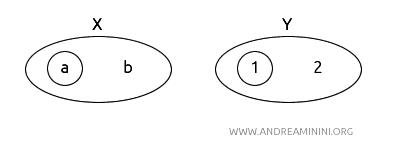
接下来检验 \( f \) 及其逆函数 \( f^{-1} \) 的连续性。

• 函数 \( f \) 的连续性
  验证 \( f \) 是否连续，需要检查 \( Y \) 中每个开集的原像在 \( X \) 中是否为开集。\( Y \) 的开集为 \(\emptyset\)、\(\{1\}\) 和 \(Y\)：
  • \( f^{-1}(\emptyset) = \emptyset \)，为开集；
  • \( f^{-1}(Y) = X \)，为开集；
  • \( f^{-1}(\{1\}) = \{a\} \)，为开集。
  因此，\( f \) 是连续的。
• 逆函数 \( f^{-1} \) 的连续性
  逆函数 \( f^{-1}: Y \to X \) 定义为 \( f^{-1}(1) = a \)，\( f^{-1}(2) = b \)。 为检验其连续性，需要确认 \( X \) 中每个开集的原像在 \( Y \) 中是否为开集。\( X \) 的开集为 \(\emptyset\)、\(\{a\}\) 和 \(X\)：
  • \( f^{-1}(\emptyset) = \emptyset \)，为开集；
  • \( f^{-1}(\{a\}) = \{1\} \)，为开集；
  • \( f^{-1}(X) = Y \)，为开集。
  因此，逆函数 \( f^{-1} \) 也是连续的。

在这种情况下，\( f \) 不仅是双射且连续，其逆函数 \( f^{-1} \) 也连续，因此 \( f \) 是一个同胚映射。

与前一个例子的不同之处在于两者所采用的拓扑结构。

说明：此例表明，通过恰当地选择 \( X \) 和 \( Y \) 的拓扑，可以使一个双射且连续的函数的逆函数也保持连续，从而成为同胚映射。而在第一个例子中，由于拓扑结构不匹配，逆函数的连续性被破坏。

同胚与其他拓扑变换的区别

虽然“同胚”常被泛指为一种拓扑变换，但严格来说，它只是拓扑变换中的一种特殊形式。

拓扑变换与同胚的关系密切，却在定义上有所区别：

• 拓扑变换
  泛指保持拓扑性质（如连通性、连续性等）的各种空间变换。除了同胚外，还包括同伦（homotopy）、同伦等价以及微分同胚（diffeomorphism）等。
• 同胚
  特指既连续又双射且逆函数连续的变换。这种映射能使两个空间在不破坏其拓扑结构的前提下相互可逆地转化。两个同胚空间在拓扑意义上是“相同”的，即使它们的几何形状可能完全不同。

因此，所有的同胚映射都是拓扑变换，但并非所有拓扑变换都是同胚映射。

某些拓扑变换虽然保持部分拓扑性质，却未必满足同胚的严格条件。

补充说明

以下是关于同胚的一些补充思考：

• 拓扑性质
  拓扑性质是指在同胚映射下保持不变的空间特征。换言之，如果两个拓扑空间是同胚的（存在连续、可逆且逆函数连续的映射），那么它们具有相同的拓扑性质。
• 豪斯多夫空间定理
  若 \( f: X \to Y \) 是同胚映射，且 \( X \) 是豪斯多夫空间，则 \( Y \) 也必然是豪斯多夫空间。换句话说，同胚会完整地保持空间的豪斯多夫性质。
• 在抽象代数中，与同胚相对应的概念是群同构。群同构保持代数结构的运算性质，而同胚保持拓扑空间中开集的结构。

通过这些例子与分析，我们更清楚地理解了同胚的意义及其在拓扑学中的重要作用。