拓扑学中的不动点

在拓扑学中，不动点指的是一个点在函数作用后位置保持不变。

换个更直观的说法：如果一个函数 f(x) 满足 f(p) = p，那么点 p 就是不动点。也就是说，在 p 处，函数的输入和输出完全相同。

$$ f(p) = p $$

可以想象一个物体绕着某个中心点 P 旋转。

旋转会改变物体上各点的空间位置，但始终存在一个特殊点不会移动，那就是旋转中心。

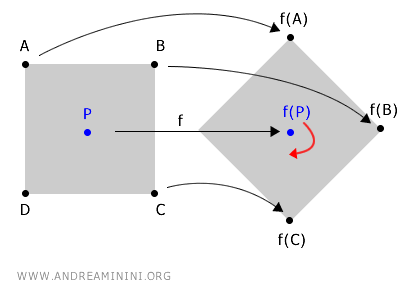
图形旋转示意图

在这个过程中，中心点 P 就是不动点。无论旋转多少次，它都保持在原来的位置。

$$ f(P) \longrightarrow P $$

不动点在数学中有广泛应用，例如数值计算中寻找方程解，博弈论中分析均衡状态，或在经济学中研究市场稳定性。在拓扑学领域，不动点思想最著名的结论之一是布劳威尔不动点定理。

直观例子

先看一个简单函数：f(x) = sin(x)，定义在闭区间 [0, 2π] 上。

$$ f(x) = \sin(x) $$

在 p = 0 时，sin(0) = 0，因此 0 是一个不动点。

$$ \sin(0) = 0 $$

在这里，不动点十分明确，函数的输入与输出完全一致。

例 2

再看 f(x) = cos(x)，仍定义在 [0, 2π] 上。

$$ f(x) = \cos(x) $$

这一次 x = 0 不再是不动点，因为 cos(0) = 1。

但这个函数依然有不动点，并且大约出现在 x = 0.73908513。

$$ \cos(0.73908513) = 0.73908513 $$

这个数值展示了不动点的存在，只是它不像前一个例子那样显而易见。

布劳威尔不动点定理指出：

任何连续函数作用在封闭的 n 维区间上时，至少存在一个不动点。

这是一个典型的存在性定理，它保证不动点一定存在，但并不要求给出不动点的位置。

这一思想在许多理论和模型中具有核心作用，例如证明动态系统是否会出现稳定状态，或说明经济模型中的均衡一定存在。

如果继续深入，还会发现不动点理论与微分方程、变分法和拓扑结构有着紧密联系。