闭集
在拓扑空间 X 中,如果对于补集 X-B 中的任意一点 u,都能找到一个邻域完全落在补集 X-B 内,那么集合 B 被称为闭集。
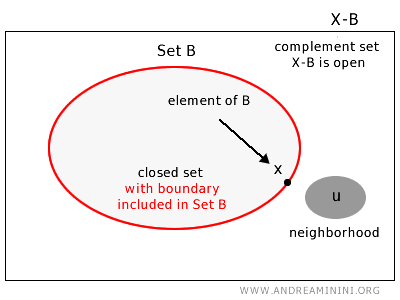
直观地理解,一个集合如果把自己的所有"边界点"都包含在内,那么它就是闭集。
形式化地说,在拓扑空间 X 中,如果集合 B 的补集 X-B 是开集,那么 B 是闭集。
注意:这意味着在闭集 B 中至少存在一些点,它们无法拥有完全包含在 B 内部的邻域。
一个基本例子
先来看实数集 R 与其中的一个闭区间。
什么是闭区间?在实数轴上,闭区间指所有满足 a≤x≤b 的点,其中 a 和 b 为实数且 a
闭区间记作 [a,b],方括号表示端点属于该集合。
例如闭区间 [3,10] 是实数轴 R 上的一个闭集。
在这个例子中,集合 B 包含从 3 到 10 之间的所有实数,包括端点 3 和 10。
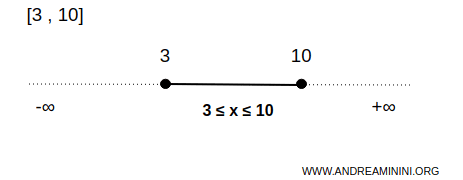
闭区间中的所有点都满足 3≤x≤10,端点自然也包含在内。
然而,在区间 [3,10] 中,并不是每个点都有一个邻域可以完全包含在区间内部。
例如端点 x=3 的任何邻域,都会有部分落在区间外。
注意:即使取极小邻域,例如 3±0.00000001,它也无法完全落在闭区间 [3,10] 内,因为 3-0.00000001 已经小于 3。端点 x=10 的情况同样如此。
这就是一维空间中最典型的闭集例子。
更多闭集示例
类似的思想可以推广到二维平面。
考虑以原点 (0,0) 为中心、半径 r=1 的圆及其内部所有点构成的集合:
$$ x^2+y^2\le 1 $$
该不等式表示所有到圆心距离不超过 1 的点,也就是说既包括圆内点,也包括圆周上的边界点。
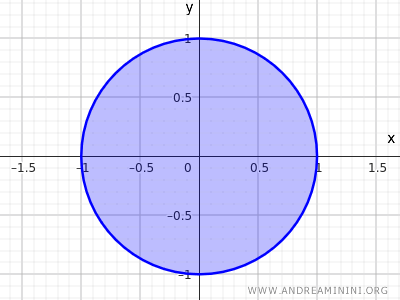
这是一个典型的平面闭集。
可以看到,圆周上的点同样无法拥有完全落在集合内部的邻域。
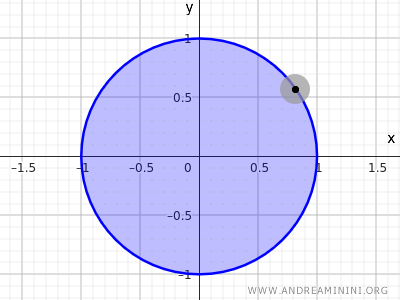
注意:在拓扑学中,仅包含圆周的集合 $x^2+y^2=1$ 在欧氏空间 R2 中既不是开集也不是闭集,因为它只包含边界点而不包含内部点。而由 $x^2+y^2\le 1$ 定义的集合则是闭集,因为它包含所有边界点。
同样的结论还可以推广到三维空间中的球面及其内部,乃至更高维空间中的 n 维球体。
闭集的补集
在空间 X 中,闭集 C 的补集 X-C 是开集。
如果集合 C 在 X 中是闭集,那么它的补集 X-C 必然是开集。
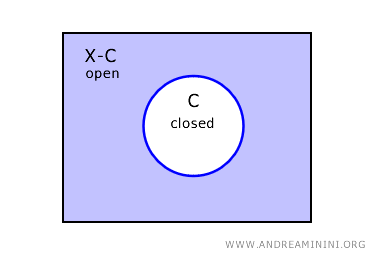
反过来,如果 U 是开集,那么 X-C 就是闭集。
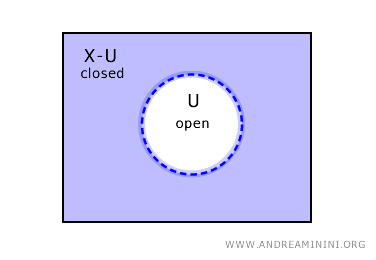
当然,还有其他情况。在拓扑空间中,可能出现既是开集又是闭集的集合,也可能出现既不是开集也不是闭集的集合。
因此,一个集合不是闭集,并不意味着它一定是开集;不是开集,也不代表它一定是闭集。
示例
考虑集合 X={a,b,c,d} 上的一个拓扑 T。
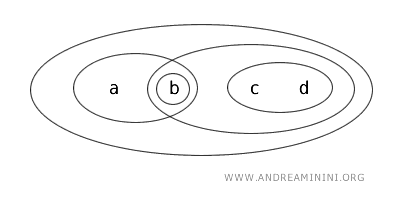
在拓扑 T 中,被定义为开集的集合包括:{b}、{a,b}、{c,d}、{b,c,d}、{a,b,c,d}、∅。
我们逐一分析如下:
- {b} 是开集,因为拓扑 T 直接将其定义为开集。
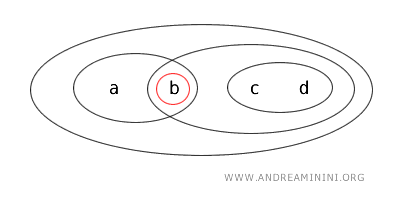
- {a} 是闭集,因为它是开集 X-{b,c,d} 的补集,其中 X={a,b,c,d}。
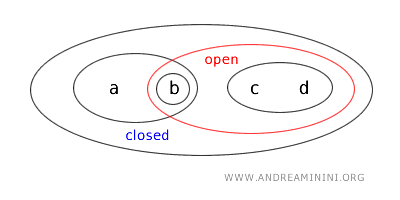
- {a,b} 既是开集又是闭集,这类集合称为"闭开集"。这种情况在实数拓扑中较少见,但在一般拓扑中完全可能,因为某些集合与其补集都属于开集。这里 {a,b} 是开集,同时作为开集 X-{c,d} 的补集,它也是闭集。
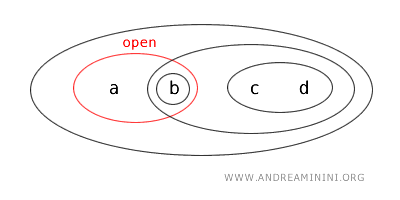
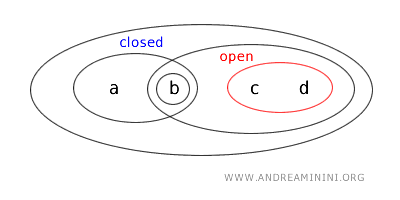
- {b,c} 既不是开集也不是闭集,它既不满足开集定义,也不是任何开集的补集。
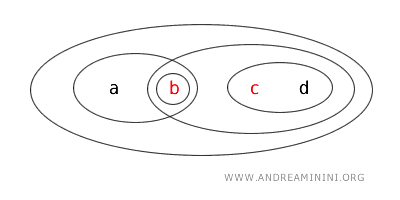
这个例子说明,在拓扑空间中,一个集合可能是开集、闭集、既是开又是闭,或者两者皆非。
闭集的性质
闭集被定义为开集的补集,并具备以下基本性质:
- 空集(记作 ∅)与整个空间 X 都是闭集。
- 任意多个闭集的交集仍然是闭集。
- 有限个闭集的并集依旧是闭集。
示例:
例如,在欧氏空间 Rn 的标准拓扑中,每一个单点集合都是闭集。
在实直线 R1 上,如果只考虑某个点 n,那么它的补集由所有不等于 n 的点构成。
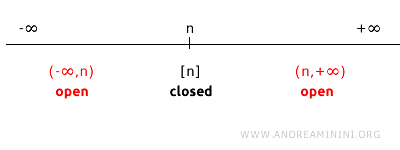
因此,单点集 {n} 的补集可以表示为两个开区间的并:(-∞, n) ∪ (n, +∞)。
由于区间 (-∞, n) 与 (n, +∞) 在标准拓扑中都是开集,它们的并集 (-∞, n) ∪ (n, +∞) 也仍然是开集。
既然 {n} 的补集是开集,我们自然可以推出 {n} 是闭集。
然而需要注意的是,单点集合并非在所有拓扑中都是闭集,其性质取决于所采用的拓扑结构。例如,在实数集 R 上定义另一种拓扑:它由所有开区间 (n, n+1)(其中 n 为整数)生成。在这种拓扑中,单点集合不是闭集,因为它不包含端点附近的邻域。
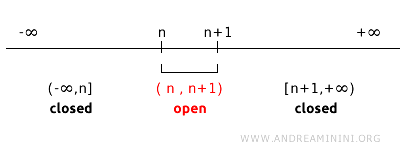
在该拓扑中,(1,2) 与 (2,3) 都被视为开集。开集 (1,2) 的补集为 (-∞, 1] ∪ [2, +∞),而开集 (2,3) 的补集则为 (-∞, 2] ∪ [3, +∞)。因此,不可能找到一个补集可以精确对应点集 {2}。一般来说,对于任意开集 (n, n+1),它的补集都是闭集 (-∞, n] ∪ [n+1, +∞)。由此可见,在该拓扑下,单点集合 n 并不被视为闭集,这清楚表明闭集的判定依赖于具体拓扑。
脚注
以下为一些补充说明与相关概念:
- 闭集与极限点
一个集合的极限点指的是:无论取多小的邻域,该邻域中总包含集合中除自身以外的至少一个点。闭集的特征在于它包含自己的全部极限点,而开集则可能遗漏这些点。示例:以实轴上的闭区间 [0,1] 为例。该区间包含所有极限点。例如点 0.5 的任意邻域中,总能找到来自区间 [0,1] 的其他点,因此 0.5 是极限点。
![0.5 为闭区间 [0,1] 的极限点示意](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
同样,端点也是极限点。例如端点 0 的任意邻域中,总包含像 0.1、0.01、0.001 等落在区间内部的点。
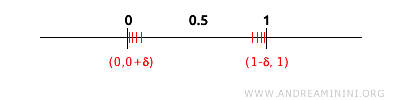
因此闭区间 [0,1] 内每个点的邻域中都包含其他属于该区间的点。 - 当且仅当 A = Cl(A) 时,集合 A 为闭集
在拓扑空间中,如果集合 \(A\) 等于它的闭包 \( \text{Cl}(A) \),即 \( A = \text{Cl}(A) \),那么 A 是闭集。闭包 \( \text{Cl}(A) \) 由集合自身以及它的全部极限点组成。因此若集合包含它所有的极限点,它就是闭集。
后续内容还可以继续展开。