拓扑学
拓扑学是数学中一门富有思想性的分支,它研究空间在连续变形下依然保持不变的性质。所谓连续变形,可以理解为拉伸、弯曲或扭转,只要不发生撕裂或粘合,空间的拓扑性质就不会改变。
因此,拓扑学关注的并不是外在的形状变化,而是在连续映射作用下始终保持不变的内在结构。
只有当出现不连续的操作时,这些性质才会发生改变,例如把空间撕开,或将原本彼此分离的部分粘合在一起。
例如,球面与立方体在拓扑意义下是等价的,因为可以在不撕裂或粘合的情况下,通过连续变形把一个逐步变成另一个。

相反,球面与环面在拓扑意义下并不等价,因为从一个变为另一个必须引入或消除一个“洞”,而这在拓扑上不可避免地意味着撕裂或粘合。
换句话说,拓扑学关心的是空间如何整体地连接在一起,而不是距离、大小或具体形状等精确的度量信息。
在拓扑学的视角中,长度、面积、体积或角度等概念并不重要。真正起决定作用的是空间的定性特征,以及不同形状之间是否能够通过连续变形相互对应。
在这一框架下,人们研究诸如连通性、紧致性、空间中“洞”的数量,以及反映空间整体结构的其他重要性质。
为此,拓扑学引入了拓扑空间的概念,其核心变换是同胚,也就是连续且可逆的映射。通过同胚,空间可以被“重塑”,但其拓扑结构始终保持不变。
正因如此,拓扑学常被形象地称为“橡皮膜几何”:人们把研究对象想象成由富有弹性的材料制成,可以拉伸、弯曲或压缩,但不能撕裂或粘合。它是现代数学中一门基础而又高度统一的重要领域。
从七座桥到一门学科
拓扑学的故事始于18世纪。数学家莱昂哈德·欧拉提出了著名的柯尼斯堡七桥问题,由此开启了对“连通性”这一概念的研究。
问题的背景很简单:在柯尼斯堡(今天的加里宁格勒),一条河流分隔出几块陆地,之间有七座桥相连。问题是 - - 有没有办法从某处出发,恰好走过每座桥一次,不重复?
七桥问题
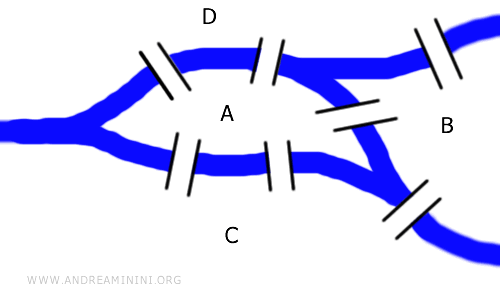
这个问题并不需要计算距离或角度,只需要考虑桥与陆地之间的连接关系。换句话说,它是一个纯粹的拓扑问题。
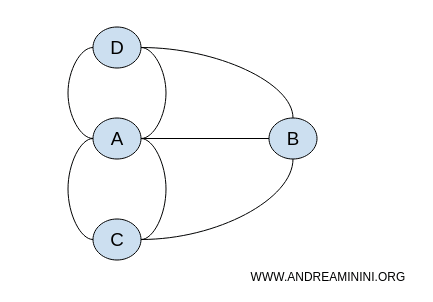
无论图形的形状如何,只要连接方式相同,它们在拓扑意义上就是等价的。
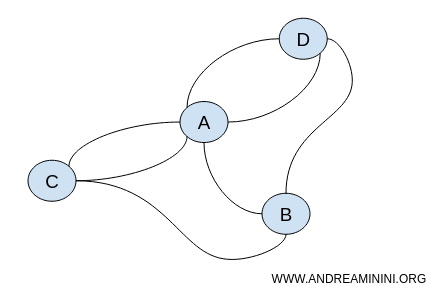
欧拉最终证明,这个问题没有解 - - 也就是说,不可能只走一遍就跨过所有的桥。这一发现标志着拓扑思想的诞生。
从那时起,数学家们开始意识到,几何不仅仅是测量与计算,还可以研究“位置”与“连接”的关系。
19世纪,高斯、缪比乌斯、李斯廷、黎曼和克莱因等人进一步发展了这些思想。李斯廷在1847年首次提出“Topology”这个词。此后,庞加莱在20世纪初创立了代数拓扑,为这一领域奠定了理论基础。
拓扑学从一开始就带有探索性的魅力 - - 它不依赖尺规,而是让我们从更高层次去理解空间的结构。
拓扑空间:形状的抽象描述
拓扑学的基础对象是拓扑空间。一个拓扑空间由集合 X 和其上的结构 T 组成,用来描述哪些点彼此“相邻”。
$$ (X,T) $$
示例:实数集 \( \mathbb{R} \) 是最常见的拓扑空间之一。如果一个集合中的每个点都有一个小区间被包含在内,那么这个集合就是“开集”。这种定义让我们能够从拓扑角度重新理解连续与极限的概念。
同胚映射:形变中的不变性
两个空间如果可以通过连续变形(不撕裂、不粘合)相互转化,我们就说它们同胚。
同胚映射是一种双向连续的变换,能保留空间的本质结构。因此,在拓扑意义上,咖啡杯和甜甜圈其实是一回事!
示例:
将咖啡杯的把手部分拉长、压扁,就能变成甜甜圈的洞。两者都只有一个孔。
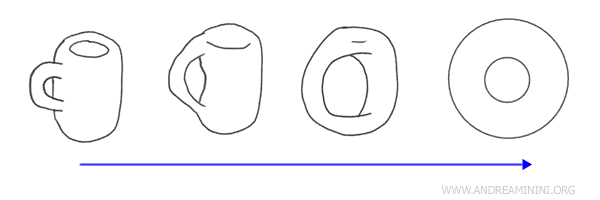
几何 vs 拓扑
几何学与拓扑学都研究形状,但视角不同:
- 几何学关注长度、角度和面积,研究“量”的变化。例如旋转、平移都是几何变换。
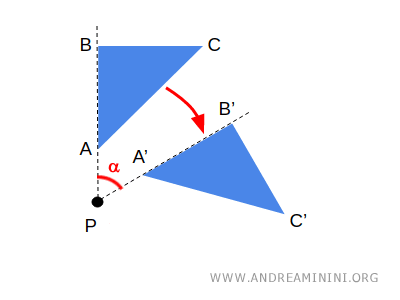
欧几里得几何以精确测量为基础,而非欧几里得几何则研究在不同公理下的空间结构。
- 拓扑学关注“形”的本质,即使经过拉伸或压缩,只要不撕裂或粘合,形状的连通关系仍保持不变。
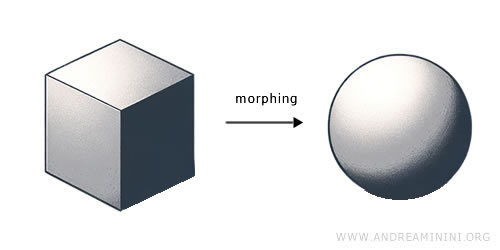
示例:将一块黏土做成的立方体慢慢压成球体,物质没有增减,只是形状改变。这就是一个典型的同胚变换。

因此,几何学关注“量的精确”,而拓扑学则探索“形的本质”。两者相辅相成,共同构成我们对空间的理解。
拓扑学的主要分支
随着研究的深入,拓扑学逐渐分化出多个方向:
- 几何拓扑:研究空间在连续变形(拉伸、收缩、折叠)下保持不变的特性。
- 一般拓扑(点集拓扑):以抽象方式研究开集与闭集、连续性、紧致性和连通性等基本概念。
- 代数拓扑:用代数工具(如群与环)来分析拓扑空间的结构。
- 微分拓扑:结合微积分研究局部类似欧几里得空间的光滑结构。
- 应用拓扑:将拓扑思想应用于数据分析、网络科学、工程与生物计算等实际问题。
拓扑学让我们跳出度量的束缚,从整体的视角理解世界。无论是数学的深层结构,还是现实世界中的复杂系统,拓扑思维都为我们提供了一种新的观察方式。
拓扑不仅是一门数学,更是一种思维方式 - - 教我们在变化中寻找不变,在复杂中发现秩序。