路径连通空间

在拓扑学中，如果一个空间 S 中的任意两点 A 和 B 都能通过一条连续曲线连接，并且这条曲线始终位于该空间内部，那么我们称 S 是路径连通的。

可以这样想象：拿一张没有边缘的纸。

这张纸代表一个连续的区域，因为不包含边界，所以我们可以把它看作一个开集。

在纸上的任意两点 A 和 B 之间，你都可以用笔直接画出一条线，而不用抬起笔离开纸面。

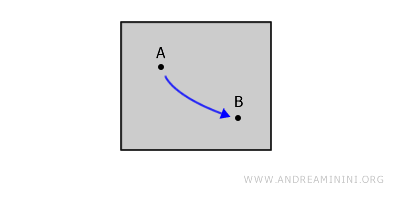
也就是说，这条路径完全处于空间内部，没有越界。

路径连通空间一定是连通空间。

这很容易理解：如果一个空间不是连通的，它就会被分成互不相连的部分，这样一来，就无法在不离开空间的前提下，用一条连续的路径把两点连接起来。

不过，反过来却不一定成立。连通空间并不总是路径连通的。

下面这个例子看起来有些反直觉，但却是拓扑学中一个经典的情形。

我们来看两个集合 Q 和 T：

$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$

$$ T = \{ \ 0 \} $$

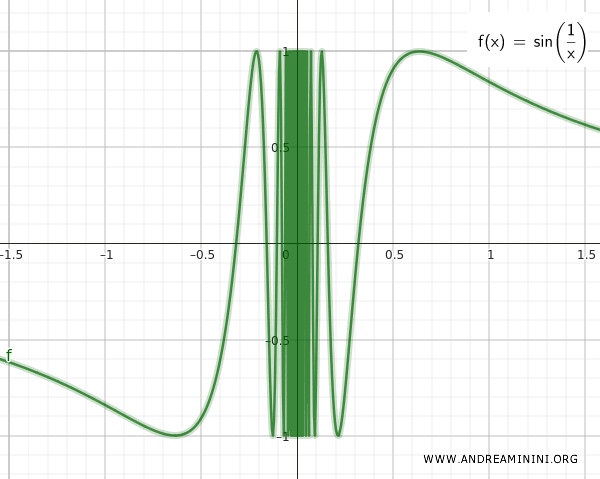
集合 Q 包含了函数 sin(1/x) 在除 0 外所有实数上的点。当 x=0 时，由于分母为零，函数值未定义。

集合 T 仅包含一个点：0。

从函数 sin(1/x) 的图像中可以看出，这两个集合 Q 和 T 无限接近。

现在我们将它们合并成一个集合：

$$ S = Q \cup T $$

集合 S 是连通的。原因在于，对于任意一个很小的 ε>0，我们都能在区间 (0-ε, 0+ε) 内找到属于 Q 的点，也就是说，0 的附近总有 Q 的点。

换句话说，0 是函数 sin(1/x) 的一个聚点。

尽管如此，S 并不是路径连通的，因为无论你如何绘制，都无法找到一条连续曲线，将 Q 中的点与 0（集合 T 中的点）连接起来。

补充说明：如果我们考虑的函数是 f(x)=1/x，情况就完全不同了。在这种情况下，集合 Q 和 T 明显是分离的，二者之间并不靠近。

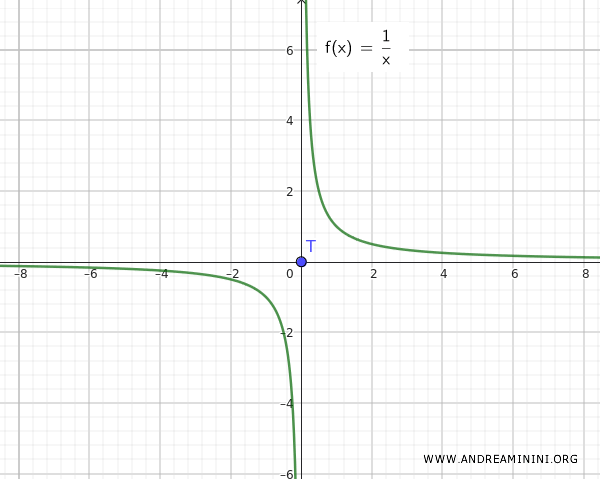
这个例子表明：当我们将连通集合 Q={∀ x ∈ R-{0}, 1/x} 与孤立点 T={0} 合并时，不一定能得到连通的结果。只有当孤立点（如 0）同时是一个聚点时，整个集合才可能连通。

拓扑学中还有许多类似的例子，它们提醒我们：连通性与路径连通性虽然相关，但并不等价。