开球（Open Ball）

在拓扑学中，开球是理解度量空间最直观、最重要的概念之一。它表示所有到某个中心点 c 的距离小于半径 r 的点所组成的集合，也叫开球体或开圆邻域。形式化表达为： $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

这里所说的度量空间 \( M \) 是一个配备了距离函数 \( d \) 的空间，这个距离函数用于衡量任意两点之间的远近关系。开球就是在这样的空间中构建拓扑结构的根本工具。

每个开球仅由两个参数决定，即中心和半径，但它们在拓扑中的作用远不止这些。开集的“开放性”意味着，在一个开球内部，总能再找到一个更小的开球，并且它完全包含在原来的开球之内，这体现了拓扑结构的局部性质。

说明: 开球在平移或缩放后仍保持其拓扑特征。也就是说，不管移动位置还是改变大小，它依然是开球，不会改变其作为开集的性质。

在二维欧氏空间 R² 中，点 p=(x,y) 到中心点 c=(x₀,y₀) 的距离由如下公式给出： $$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

基于这一定义得到的开圆邻域，构成了平面上标准拓扑的基本框架。可以说，R² 的拓扑结构几乎完全依赖这些开球来描述。

R² 的标准拓扑可以理解为由所有可能的开球组合而成的整体结构：

$$ B = \{ B(p, r) \ | \ p \in R^2,\ r > 0 \} $$

其中 p 是平面上的任意点 p=(x,y)，r 是半径。

虽然对平面可以定义很多不同的拓扑，但标准拓扑是最自然、最常用的一种，也是微积分与几何的基础概念所依赖的结构。

开球还有一个非常关键的性质。对任意一个开球 B(p,r)，只要选取其中一点 $ q \in B(p,r) $，都可以构造一个以 q 为中心的更小开球 B(q,ε)，并且它完全包含在原来的开球内：

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ such \ that \ B(q,ε) \subset B(p,r) $$

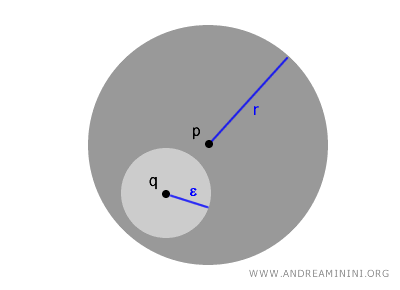
这种层层嵌套的结构，是理解度量空间拓扑的核心。它不仅揭示了开集的本质，也为进一步学习连续性、极限和拓扑基奠定了基础。