Внутренняя часть множества

В топологическом пространстве \( X \) внутренняя часть множества \( A \) определяется как объединение всех открытых подмножеств, полностью содержащихся в \( A \). Обычно для её обозначения используют \( \text{Int}(A) \) или \( A^\circ \).

Говоря неформально, внутренняя часть множества - это самая большая «открытая область», целиком лежащая внутри множества \( A \).

Ни одно открытое подмножество, содержащееся в \( A \), не может быть больше его внутренней части.

Примечание: Поскольку внутренняя часть определяется как объединение открытых множеств, она сама всегда является открытым множеством.

В строгом смысле внутренняя часть множества \( A \) состоит из всех тех точек \( A \), для которых можно найти открытую окрестность, целиком лежащую в \( A \).

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ является открытым в } X \} $$

Иначе говоря, точка \( x \) принадлежит внутренней части множества \( A \) тогда и только тогда, когда существует открытое множество \( U \), содержащее \( x \) и полностью включённое в \( A \).

Важно понимать, что внутренняя часть множества $A$ определяется топологией пространства $X$, в котором рассматривается множество $A$, а не собственными свойствами самого множества $A$. Поэтому при изменении топологии внутренняя часть одного и того же множества может изменяться.

Практический пример

Рассмотрим множество \( A = [0, 1] \) в пространстве \( \mathbb{R} \) со стандартной топологией.

Этот отрезок содержит все вещественные числа от 0 до 1, включая граничные точки.

В этом случае внутренняя часть множества \( A \) совпадает с открытым интервалом \( (0, 1) \).

$$ \text{Int}(A) = (0,1) $$

Это наибольший открытый интервал между 0 и 1. Точки 0 и 1 не входят во внутреннюю часть, так как ни одна из них не принадлежит открытому интервалу, полностью лежащему внутри \( A \).

Пример 2

Теперь рассмотрим множество \( A = [0, 1) \) в \( \mathbb{R} \) при той же стандартной топологии.

Этот интервал замкнут слева и открыт справа, он содержит все вещественные числа от 0 включительно до 1 не включая её.

Несмотря на это, внутренняя часть множества \( A \) остаётся той же, что и в предыдущем примере:

\[ \text{Int}(A) = (0,1) \]

Причина в том, что внутренняя часть определяется через открытые подмножества, полностью содержащиеся в исходном множестве.

Примечание: В \( \mathbb{R} \) со стандартной топологией базу топологии образуют открытые интервалы. Поэтому максимальным открытым подмножеством, содержащимся в \( [0, 1) \), является именно интервал \( (0,1) \). Точка 0 не входит во внутреннюю часть, так как она не принадлежит ни одному открытому интервалу, целиком лежащему в \( A \).

Пример 3

Рассмотрим теперь то же множество \( A = [0,1) \), но в пространстве \( X \) с дискретной топологией.

В дискретной топологии каждое подмножество пространства \( X \) считается открытым.

Это означает, что для любой точки множества \( A \) существует открытая окрестность, полностью лежащая в \( A \), причём выбор такой окрестности ничем не ограничен.

При дискретной топологии на \( \mathbb{R} \) открытыми считаются все подмножества: открытые и замкнутые интервалы, произвольные наборы точек, пустое множество и само множество \( [0,1) \). Например, множества \( (0,0.5) \), \( (0.25,0.75) \), \( (0,1) \) и даже \( [0,0.25] \), лежащее внутри $ A=[0,1) $, являются открытыми.

Поскольку множество \( A = [0,1) \) само является открытым, его внутренняя часть совпадает с ним целиком.

$$ \text{Int}(A) = A = [0,1) $$

В дискретной топологии внутренняя часть любого множества всегда равна самому этому множеству.

Примечание: Этот пример хорошо показывает, насколько сильно выбор топологии влияет на свойства множеств. Характер окрестностей и внутренней части определяется не самим множеством, а топологической структурой пространства \( X \).

Пример 4

Рассмотрим топологическое пространство \( X = \{a, b, c\} \) с дискретной топологией.

В таком пространстве любое подмножество является открытым:

• Множества \( \emptyset \) и \( \{a, b, c\} \) открыты по определению.
• Одноточечные множества \( \{a\} \), \( \{b\} \) и \( \{c\} \) также открыты.
• Множества, состоящие из двух точек, например \( \{a, b\} \), \( \{a, c\} \) и \( \{b, c\} \), являются открытыми как объединения открытых множеств.

Пусть \( A = \{b, c\} \) - подмножество пространства \( X \).

По определению внутренняя часть \( \text{Int}(A) \) является объединением всех открытых подмножеств, содержащихся в \( A \).

В данном случае такими подмножествами являются \( \{b\} \), \( \{c\} \) и \( \{b, c\} \).

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Следовательно, внутренняя часть множества \( A \) совпадает с самим множеством \( A \).

Примечание: Этот вывод справедлив для любого подмножества \( S \subseteq X \) в дискретном топологическом пространстве. Поскольку все подмножества открыты, всегда выполняется равенство \( \text{Int}(S) = S \).

Теорема о внутренней части множества

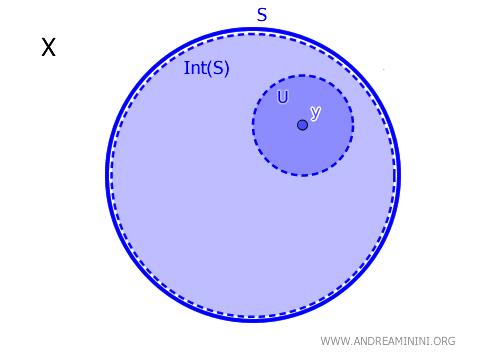
Пусть $X$ - топологическое пространство, $S \subseteq X$ - подмножество, а $y \in X$ - точка. Точка $y$ прhttps://www.ecoage.org/ru/math/ru-how-to-determine-the-interior-of-a-set-in-rинадлежит внутренней части множества $S$, обозначаемой $\operatorname{Int}(S)$, тогда и только тогда, когда существует открытое множество $U$ такое, что $y \in U \subseteq S$. Иначе говоря, $$ y \in \operatorname{Int}(S) \iff \exists \ U \text{ - открытое множество, для которого } y \in U \subseteq S $$

Проще говоря, точка принадлежит внутренней части множества, если вокруг неё можно «помес/ru/math/ru-the-intersection-of-set-interiorsтить» открытую окрестность, которая целиком лежит внутри этого множества.

Эта теорема даёт удобный и наглядный критерий, позволяющий определить, является ли данная точка внутренней для множества в топологическом пространстве.

Доказательство

• Необходимость: Если точка \( y \) принадлежит внутренней части множества \( S \), то по самому определению внутренней части существует открытое множество \( U \), содержащее точку \( y \) и целиком лежащее в \( S \). Тем самым условие существования такого множества \( U \) является обязательным.
• Достаточность: Если существует открытое множество \( U \), для которого выполняется \( y \in U \subseteq S \), то точка \( y \) автоматически принадлежит внутренней части множества \( S \), поскольку внутренняя часть определяется как объединение всех открытых подмножеств, содержащихся в \( S \).

Примечание: Теорема играет важную роль в топологии, так как связывает понятие внутренней точки с понятием открытого множества. Это делает её особенно полезной при изучении непрерывных отображений и локальных свойств пространств.

Пример

Рассмотрим множество \( A = [1, 3] \) в топологическом пространстве \( \mathbb{R} \) со стандартной топологией.

$$ A = [1,3] $$

Это замкнутый отрезок на вещественной прямой, включающий все числа от 1 до 3.

Определим его внутреннюю часть с помощью сформулированной теоремы.

Для этого найдём открытое множество \( U \), полностью содержащееся в \( A \).

1. Выбор множества \( U \)
   Возьмём интервал \( U = (1, 3) \). Он является открытым в стандартной топологии на \( \mathbb{R} \).
2. Проверка включения
   Каждая точка интервала \( (1, 3) \) принадлежит отрезку \( [1, 3] \). Граничные точки 1 и 3 не входят в \( U \), поскольку открытые интервалы не содержат концов.

Следовательно, множество \( U \) является открытым и целиком лежит внутри \( A \). Это означает, что внутренняя часть множества \( A \) равна интервалу \( (1, 3) \).

Примечание: Точки 1 и 3 не являются внутренними точками множества \( A \), так как для них не существует открытой окрестности, полностью содержащейся в \( A \).

Свойства внутренней части

Внутренняя часть множества обладает рядом важных свойств, которые показывают, как она взаимодействует с другими топологическими операциями, такими как объединение, пересечение и замыкание.

• Объединение внутренних частей
  Объединение внутренних частей двух множеств всегда содержится во внутренней части их объединения: $$ \operatorname{Int}(A) \cup \operatorname{Int}(B) \subseteq \operatorname{Int}(A \cup B) $$
• Пересечение внутренних частей
  Внутренняя часть пересечения двух множеств совпадает с пересечением их внутренних частей: $$ \operatorname{Int}(A) \cap \operatorname{Int}(B) = \operatorname{Int}(A \cap B) $$
• Внутренняя часть дополнения
  Внутренняя часть дополнения множества \( A \) равна дополнению его замыкания: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A) $$
• Дополнение внутренней части
  Замыкание дополнения множества \( A \) совпадает с дополнением его внутренней части: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A) $$

Заметки

Ниже приведены некоторые полезные следствия и дополнительные наблюдения.

• Если U открыто и U ⊆ A, то U ⊆ Int(A)
  Любое открытое множество, целиком содержащееся в \( A \), автоматически является частью его внутренней части.
• Если A ⊆ B, то Int(A) ⊆ Int(B)
  Операция взятия внутренней части сохраняет включение множеств.
• Множество открыто тогда и только тогда, когда оно совпадает со своей внутренней частью
  Это свойство часто используют как практический критерий открытости множества.
• Вычисление внутренней части множества с помощью языка R
  Язык R может применяться для численного анализа и моделирования топологических понятий в прикладных задачах.

И так далее.